首先，先介绍一些计算几何的基本知识。

# 计算几何基础

既然是几何，显然，我们有着与几何类似的点线面。在我看来这更像是解析几何：

我们定义 Point 为：

struct Point{
    double x, y;

    Point(double _x=0, double _y = 0){
        x = _x, y = _y;
    }
    
    Point operator + (const Point& a){
        return Point(x + a.x, y + a.y);
    }
    
    Point operator - (const Point& a){
        return Point(x - a.x, y - a.y);
    }
    
    double operator * (const Point& a){
        return x * a.x + y * a.y;
    }
    
    Point operator * (const double& a){
        return Point(a * x, a * y);
    }
    
    Point operator / (const double& a){
        return Point(a / x, a / y);
    }
    
    double operator ^ (const Point& a){
        return a.y * x - a.x * y;
    }
    
}

typedef Point Vector;

这样，我们定义了点与向量，并且重定义了运算符号，如内积与外积。

其中，我们可以使用外积来判断两个向量之间的位置关系：

1. 若 $\vec{a} \times \vec{b} > 0$， 则 $\vec{a}$ 在 $\vec{b}$ 的顺时针方向
2. 若 $\vec{a} \times \vec{b} < 0$， 则 $\vec{a}$ 在 $\vec{b}$ 的逆时针方向
3. 若 $\vec{a} \times \vec{b} = 0$， 则 $\vec{a}$ 与 $\vec{b}$ 共线

如此，我们便可以定义直线 Line

struct Line{
    Point x, Point y;
    double a, b, c;
    
    Line(Point _x, Point _y){
        x = _x, y = _y;
        a = _x.y - _y.y;
        b = _y.x - _x.x;
        c = _x.x * _y.y - _y.x * _x.y;
    }
}

那么，我们可以这样判断两条直线是否相交：

bool judge(Line p, Line q){
    Point a = p.x, b = p.y, c = q.x, d = q.y;
    if(((b - a) ^ (c - a)) * ((b - a)^(d - a)) < 0 &&
      ((c - d) ^ (c - a)) * ((c - d) ^ (c - b)) < 0)
        return true;
    return false;
}

也就是说 $$ \vec{ab} \times \vec{ac} \text{与} \vec{ab} \times \vec{ad} \text{异号，即} d, c \text{两点在线段} p \text{的两侧}\ \vec{dc} \times \vec{ac} \text{与} \vec{dc} \times \vec{bc} \text{异号，即}a,b\text{两点在线段} q \text{的两侧}\ $$ 画图表示为：

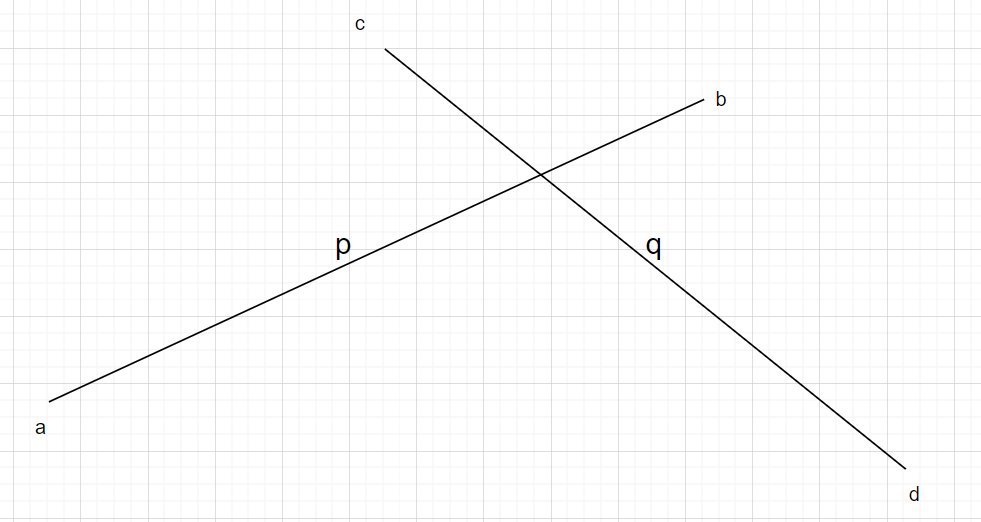
# 判断点是否在多边形内部

有了点与向量的定义后，我们就可以构造一个多边形了

vector<Point> p;

我们假设这个 vector 中按照一定次序（顺时针或逆时针）存储着多边形的顶点。

我们如何判断一个点是否在多边形内部呢？

我们使用射线法来判断。具体而言：

我们从目标点出发引一条射线，看这条射线和多边形所有边的交点数目。如果有奇数个交点，则说明在内部，如果有偶数个交点，则说明在外部。但有一些极端情况如下图所示。

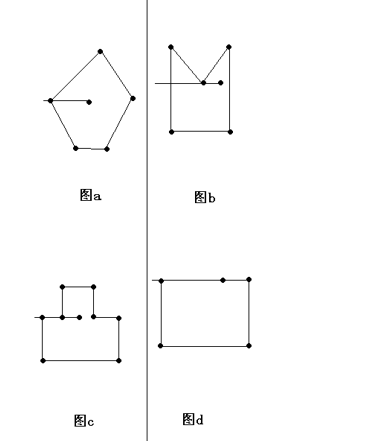
在图(a)中，L和多边形的顶点相交，这时候交点只能计算一个；在图(b)中，L和多边形顶点的交点不应被计算；在图(c)和(d) 中，L和多边形的一条边重合，这条边应该被忽略不计。

# 凸包

什么是凸包？简单的理解就是给你一些点，凸包就是能够让所有点都在一个多边形内（在边上也算内）的最小的多边形。这里的最小指面积最小

这里讲一个比较简单的算法 Graham 算法。

我们通过下图来解释算法流程：

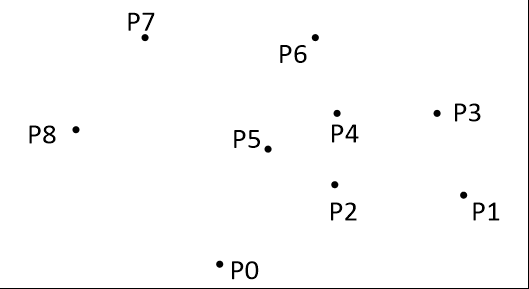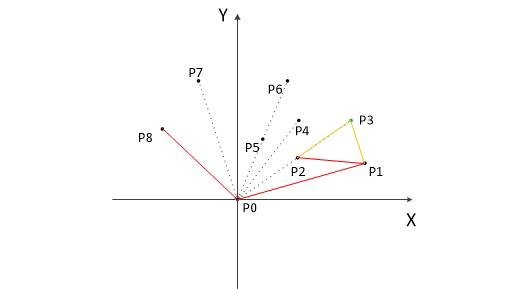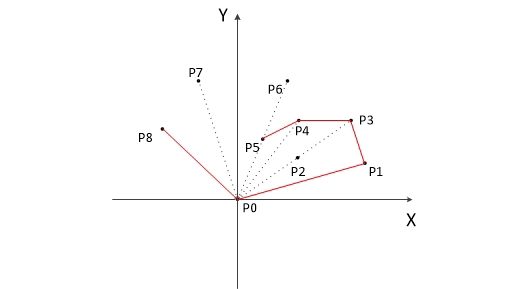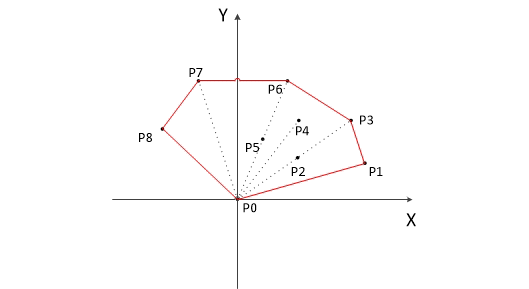
我们首先会先将点按照极角的大小顺序排列，接着按顺序遍历每个点，通过夹角的大小判断哪些点在凸包上。具体而言：

1. 首先求出最左下角的点，设为 $p_0$，其余的点我们按照与 $p_0$ 的极角大小，逆时针排序，得到 ${p_1, p_2,\dots, p_n}$
2. 令栈 $S = \empty$，其中 $S[i]$ 表示栈中的第 $i+1$ 个元素，用 $k$ 表示栈中的元素个数；若栈中有 $k$ 个元素，则 $S[k−1]$ 即为栈顶元素；每一次push，栈元素个数 $k + 1$ ；每次pop，栈元素个数 $k - 1$
3. $push(S, p_0)$
4. $push(S, p_1)$
5. 遍历集合 ${p_2, p_3, \dots, p_n}$， 遍历栈，如果 $k \geq 2$ 并且由向量 $\overrightarrow{S[k-2]p_i}$ 与向量 $\overrightarrow{S[k-2]S[k-1]}$ 构成的夹角 $\theta \geq 180$，$pop(S)$
6. 否则 $push(S,p_i)$

最后，如果 $S$ 的大小小于3，那么我们无法生成一个凸包，否则 $S$ 就构成了一个凸包的顶点集合。

# 算法复杂度

显然，算法的复杂度是 $O(nlogn)$ 其中 $n$ 是点集的大小。

# 碰撞检测算法（GJK）

碰撞检测，在游戏与自动驾驶等等领域都有应用。这里介绍一种非常常用的算法：GJK ，用于检测 2D 平面内凸多边形的碰撞。

首先我们思考，当两个物体碰撞，发生部分重叠的时候，我们是怎样让计算机知道他们发生了碰撞呢？

假设这两个多边形如下：

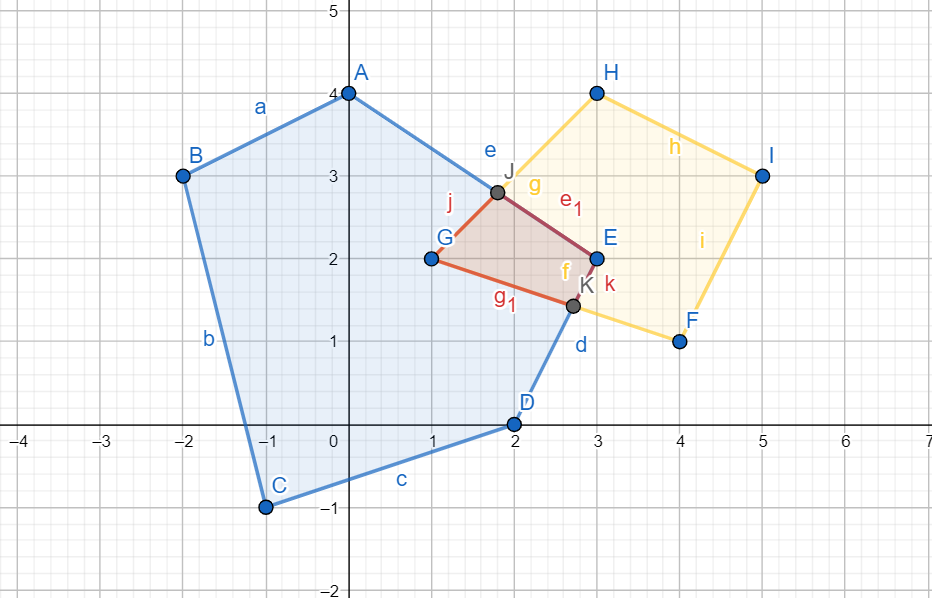
我们知道，两直线相交的交点是同时处于这两条直线上的，也就是说，这两条直线享有一个共同的坐标。

而对于重叠部分的平面而言，我们可以类比知道，这两个发生重叠的多边形，一定有着一组点共享一组坐标。

产生碰撞的条件就是两个图形至少重合一个点，否则我们认为碰撞没有发生。而重合的点相减后必为 $(0, 0)$

因此，问题就转化为：能否从两个图形中各自找到一个点，使得他们相减后为$(0, 0)$

这就是 GJK 算法的核心问题。

计算机想要“看见”两个图形重叠的部分，可以遍历左边所包围的所有坐标 减去 右边的坐标，得到一系列的点。将这些点全部包围起来，如果这个新生成的图形 包含原点，则意味着两个图形发生了重叠，从而判断两个图形发生了碰撞。我们把计算后的点称为 闵可夫斯基差 ，将生成的三角形/线性称为 单纯形。

但这样的做法是很费时间的，因为可能图形非常大从而我们没办法在短时间内就算出闵可夫斯基差。因此我们利用凸多边形的特点，将他们的顶点相减就可以达成我们的目的。

但即便这样，我们需要计算的点也是很多的（因为我们需要计算任意两个顶点之间的差），因此，GJK 算法采用了另一个思路。

我们定义了一个名为 support 的函数，具体而言它将：

1. 我们设定一个向量 $\vec{u}$ ，将黄色多边形的所有顶点投影到这个方向，求出最大点
2. 将向量取反，然后将蓝色多边形的所有顶点投影到取反后的方向上，求出最大点
3. 将得到的两个点相减，即可得到单纯形上的一点

事实上，我们就是延长了向量 $u$ ，并过多边形的顶点做 $u$ 的垂线，垂足即为投影点。

如下图所示：

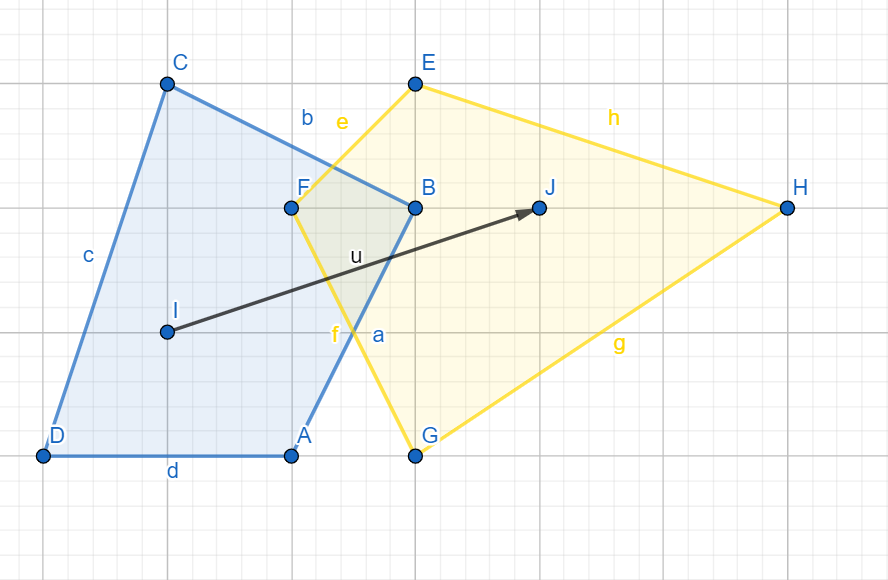
第一次迭代后，我们得到如下结果：

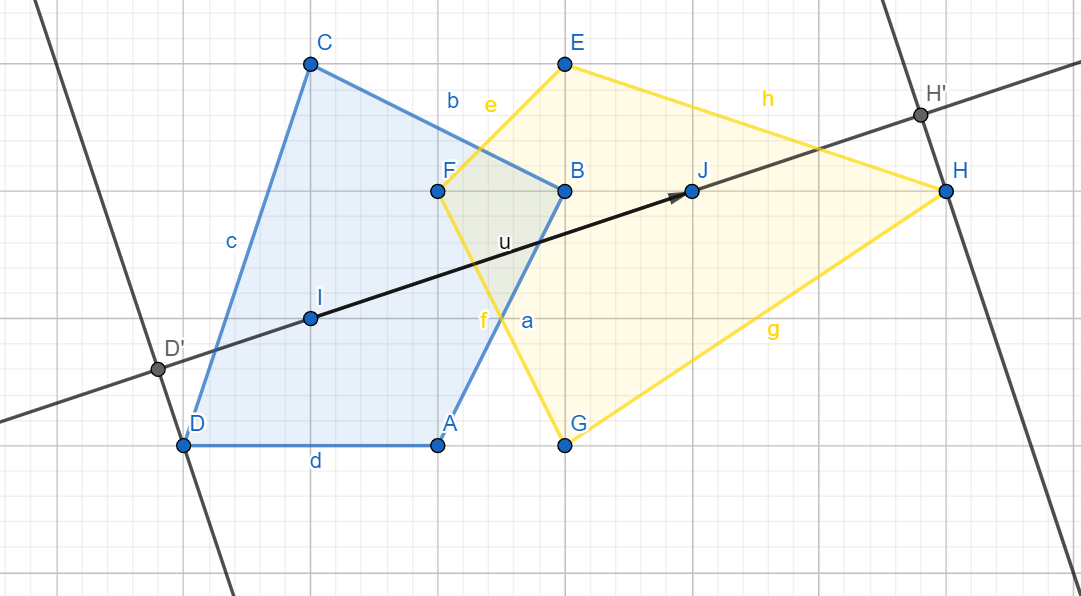
最大点坐标分别为 $(8, 5), (2, 3)$ 即 $H, D$ 的坐标

于是我们得到单纯形的一个顶点为 $(6, 2)$

第二次，我们将 $u$ 取反，然后再做一次这三个工作，得到如下图所示：

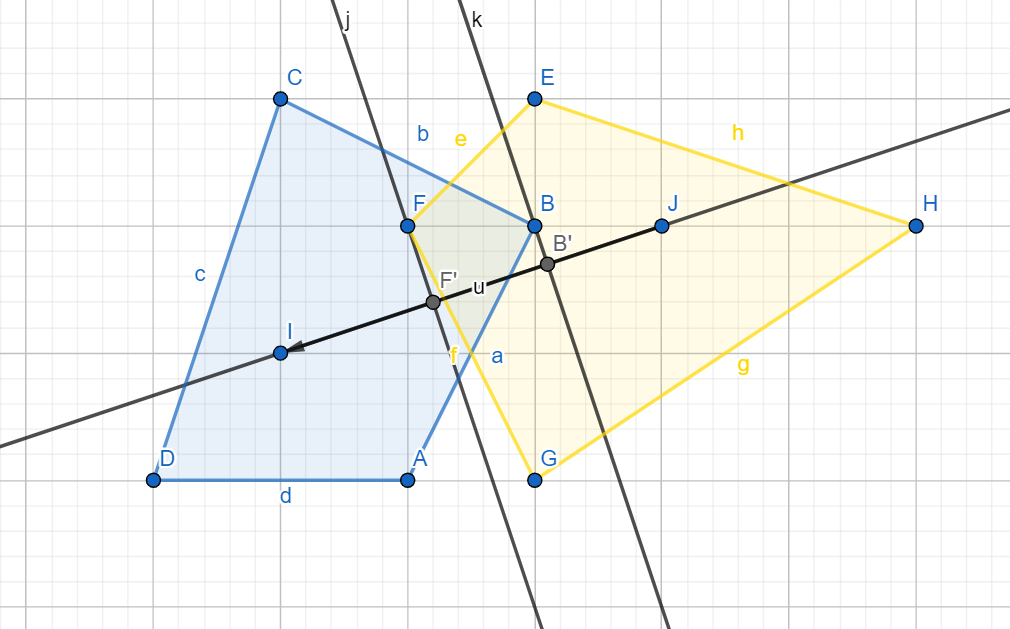
注意最大的定义是沿着向量 $u$ 的投影值最大，需要考虑正负的

于是，我们得到了最大点坐标为 $(4, 5), (5, 5)$ ，即 $F, B$ 的坐标。

那么，我们得到第二个单纯形的坐标为 $(4, 5) - (5, 5) = (-1, 0)$

第三次迭代，我们取与 $\vec{u}$ 垂直的向量 $\vec{v}$ 作为新的方向向量，我们任取一个方向即可，随后还是做相同的迭代：

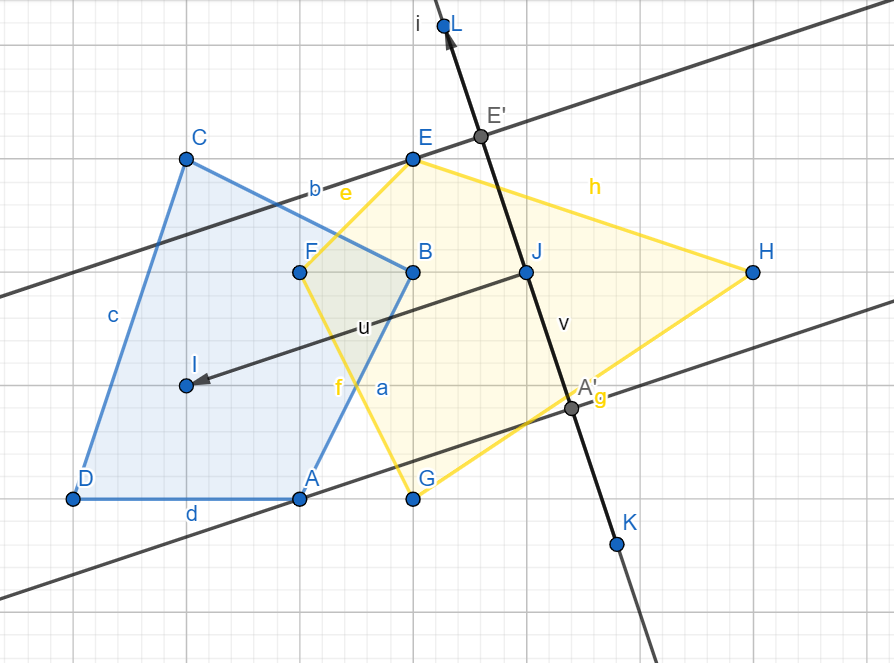
于是，我们得到 $(5, 6), (4, 3)$，即点 $E, A$

那么，我们得到了单纯形的第三个顶点 $(5, 6) - (4, 3) = (1, 3)$

现在，我们可以开始构造单纯形了，如图：

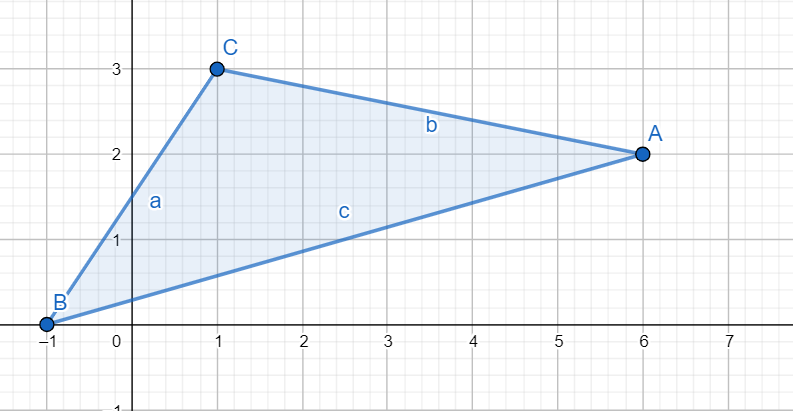
我们似乎并没有能够包涵原点，但如果我们 $\vec{v}$ 选择了另一个方向，就能够生成一个能包涵原点的单纯形。因此方向并不是真的任意选的。

但一般情况下，我们可能三次迭代就得到一个符合条件的单纯形吗？

显然是不行的，大部分情况下我们都需要更多的迭代次数，因此我们需要改变 support 函数的方向。

如何改变呢？

如图：

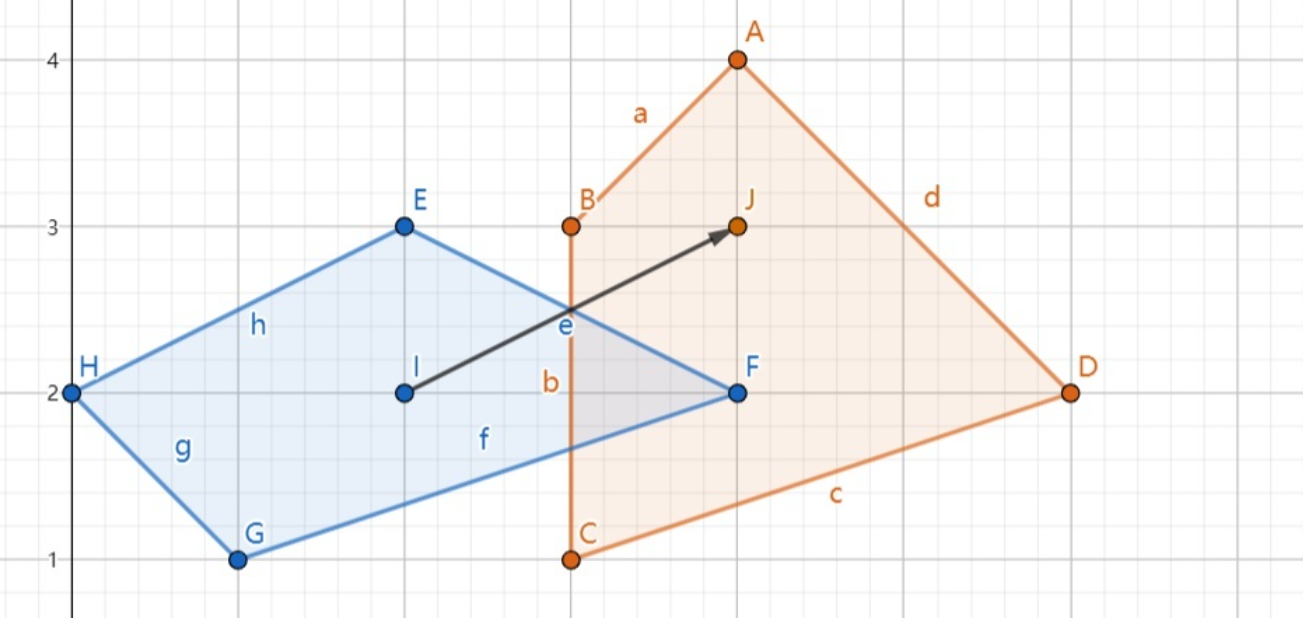
最开始，我们还是随机选一个向量 $\vec{u}$ ，然后迭代两次，计算出单纯形的两个顶点，这里是 $(6, 0), (1, 1)$

随后，我们得到了一个一维单纯形（一个线段），然后我们做这个单纯形的中垂线：

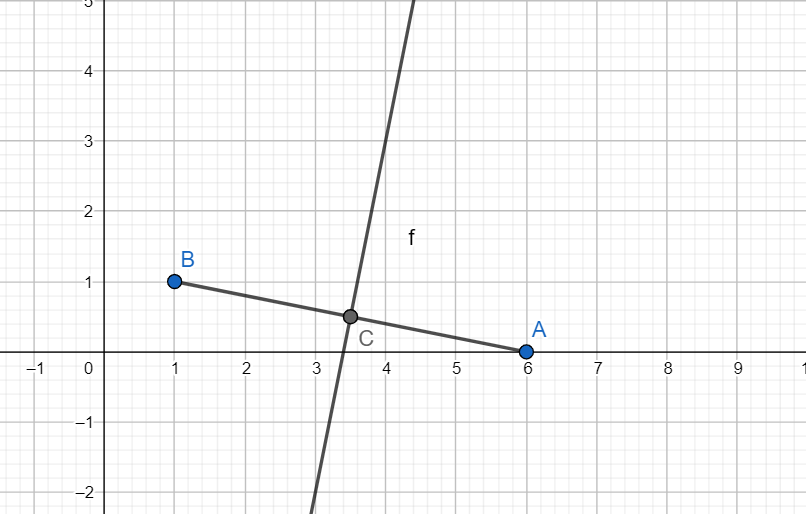
可以发现，我们得到了两个向量，一个朝向原点，一个背离原点。由于前面的教训，我们知道方向的选择是有讲究的，论文中都选择了指向原点的向量作为下一次迭代时的方向向量（因为这样更有可能构成包含原点的单纯形）。

下一次迭代后，我们得到单纯形的第三个顶点为 $(1, -2)$ ，于是构建单纯形为：

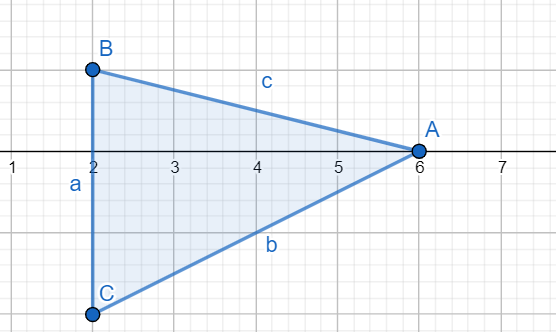
然而，这个单纯形并没有包含原点。因此，我们在这个单纯形中，找到最靠近原点的一条边，并计算出一个与这条边垂直的向量，重新构造二维单纯形，选取的方向向量仍然是朝向原点的。在这里，我们需要删除 $A$ 点，留下 $BC$ 边做垂线，得到一个指向原点的向量作为下一次迭代的方向向量（这个例子中应当是与 x 轴相反方向的向量）

最后，我们就能够构建出一个包含原点的单纯形（注意，原点在单纯形边上也算是包含）

# 如何退出迭代

察觉到没有碰撞的时候就会推出迭代，那么是如何进行判断的呢？

我们知道，在第三次迭代时，会计算一个单纯形的顶点，我们记为 support 点，若这个点与迭代方向的内积小于0，说明这个迭代方向上已经无法找到一个能够跨越原点的 support 点了，也就是说无法组成一个包含原点的单纯形，也就是说两个多边形不相交，那么就可以结束迭代了。

内积小于0，表示两个向量不同方向