匈牙利算法主要被用于解决一些与二分图匹配有关的问题。

# 二分图

二分图是一类特殊的图，它可以被划分为两个部分，每个部分的点互不相连，如下如图所示：

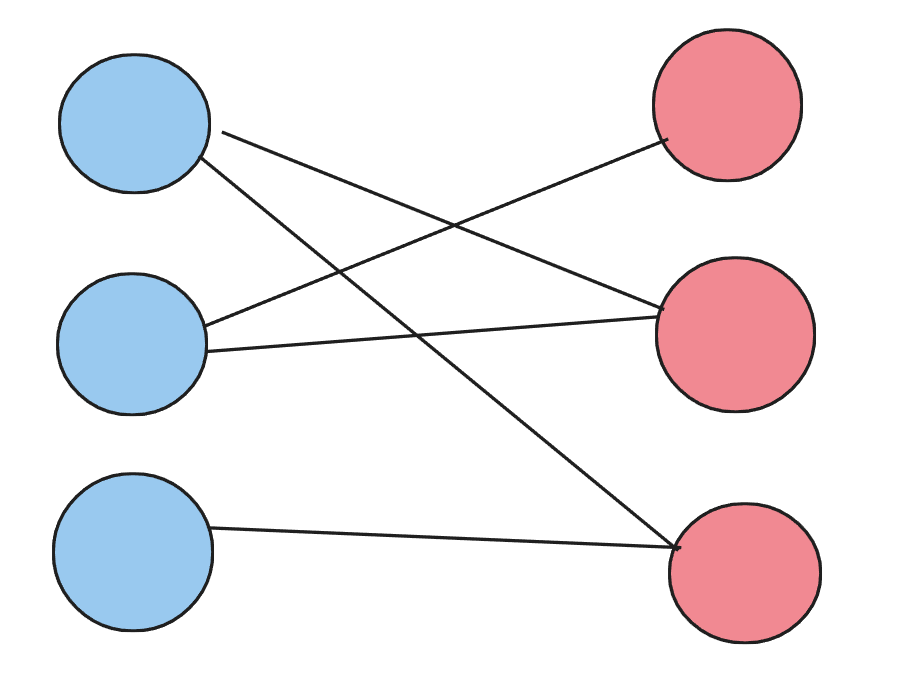
这样就是一个典型的二分图，可以看见，每条边的端点都分别处于左侧集合与右侧集合中。

# 最大匹配问题

形式化的问题可能会比较抽象，我们用一个经典的例子来引入：

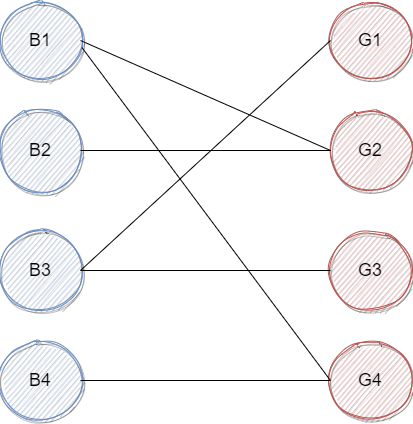
这个二分图，我们可以视为男生与女生的两个集合，边表示他们之间可能互相比较对眼。

最大匹配问题可以被视为：如果他们去参加一个舞会，舞会要求必须一男一女搭配（舞伴当然是从对眼的人里面选择了），这个时候，你最多能找出多少对舞伴？

# 算法过程

显然，我们可以肉眼看出，最多能找出来3对，但对于复杂一些的图来说，我们就没办法一眼看出来了，这个时候我们来看看匈牙利算法是怎么运行的。

首先，我们从 $B_1$ 开始，我们查看与他有连线的女生，发现他与 $G_2$ 可以，于是我们暂把他与 $G_2$ 相连（注意这时候的所有安排都是暂时的，可以被撤销），于是，我们得到下图：

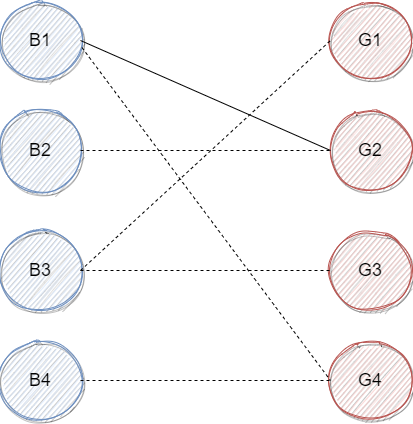
然后我们观察 $B_2$ ，发现 $B_2$ 也与 $G_2$ 有连线，但这个时候 $G_2$ 在我们的设想中已经与 $B_1$ 配对了，那怎么办？

我们倒回去看 $G_2$ 的配对对象 $B_1$ ，观察对 $B_1$ 而言有没有其他的选项的？我们发现是有的，是 $G_4$ ，并且 $G_4$ 暂时还没有任何舞伴，于是我们擦除 $(B_1, G-2)$，连接上 $(B_1, G_4), (B_2, G_2)$，如下图：

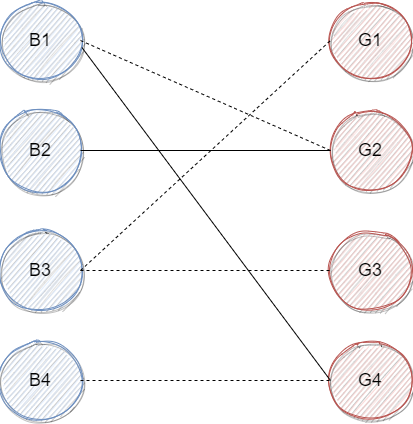
接着到 $B_3$ ，可以直接与 $G_1$ 配对。而至于 $B_4$，我们发现他只能与 $G_4$ 配对，但 $G_4$ 已经成为了 $B_1$ 的舞伴。虽然 $B_1$ 还能选择 $G_2$，但 $G_2$ 已经与$B_2$ 配对了并且 $B_2$ 不能与其他女生配对了。

我们绕了这么大一圈发现，我们没办法改变其他人的配对对象了，那么 $B_4$ 就只能一个人跳舞了，最终的配对如下图：

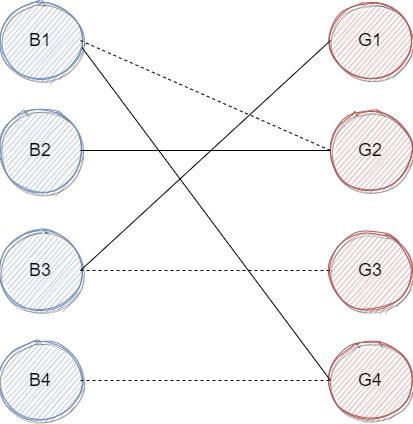
这就是匈牙利算法的流程了。

# 代码实现

const int N = 505;
int m, n; //m,n 分别表示左、右侧集合的元素数量
int graph[N][N]; //邻接矩阵存图
int p[N];         
bool vis[N];
bool match(int i){
    for (int j = 1; j <= n; ++j)
        if (graph[i][j] && !vis[j]) { // 有边存在且 j 未被访问过
            vis[j] = true;                 
            if (p[j] == 0 || match(p[j])) { // 如果暂无匹配对象 || 原来匹配的左侧对象可以找到新的匹配
                p[j] = i;    // 当前左侧元素成为当前右侧元素的新匹配
                return true; 
            }
        }
    return false; 
}
int Hungarian(){
    int cnt = 0;
    for (int i = 1; i <= M; ++i){
        memset(vis, 0, sizeof(vis));
        if (match(i))
            cnt++;
    }
    return cnt;
}

# 算法复杂度

可以发现，匈牙利算法以顶点集合 $V$ 为基础，每次从 $X$ 集合中选取一个顶点 $X_i$ 作为搜索起点，并且都使用了 dfs 来搜索边集 $E$ 中的所有边。于是，我们可以得到复杂度为 $O(|V|\times |E|)$