# 导引

我们从一个简单的例子看起：Fib(n) 斐波那契数列。 $$ Fib(n) = \begin{cases} 1, \quad n = 0,1 \ Fib(n-1) +Fib(n-2), \quad otherwise \end{cases} $$ 我们很容易写出一个递归函数

def f(n):
    if n <= 1:
        return 1
    else:
        return f(n - 1) + f(n - 2)

但这种写法我们已经被告知：“啊这种肯定不行啊，算个 Fib(100) 电脑就能煎鸡蛋了”。

这个最大的问题其实是会发生 Stack Overflow。

在大多数语言中，函数的调用过程如下图所示：

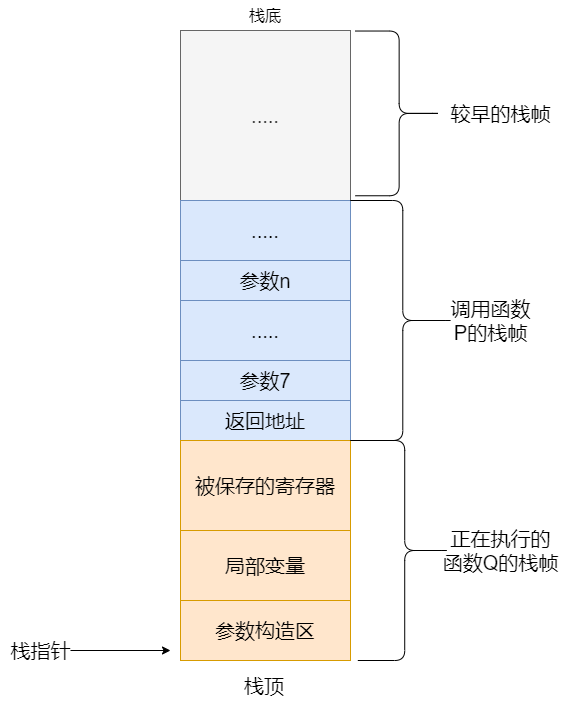
这个栈就是一个进程的栈空间，一个进程的内存空间是有限的：

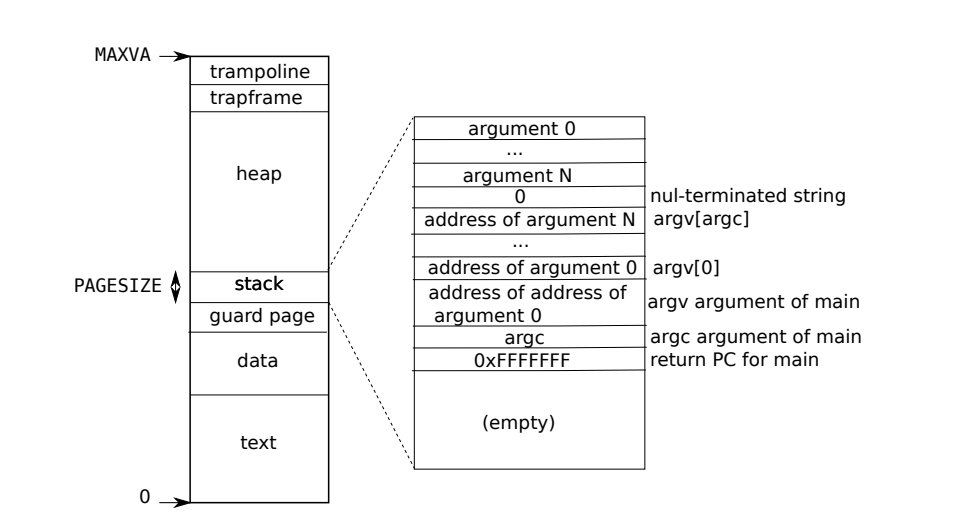
所以栈空间是很宝贵的，当我们使用上面的递归进行计算时，当 $n$ 较大时会发现我们调用的函数层数太深，每调用一次函数都会增加一个栈帧，于是 Stack Overflow 就成为了必然的事情。

所以我们想知道，有没有一种方法可以避免这种事情的发生呢？

有的，迭代是一个常见的方法。但有些时候，一些问题的递归写法更直观，那么我们就可以通过尾递归的方式来实现。

# 尾递归优化

若函数在尾位置调用自身（或是一个尾调用本身的其他函数等等），则称这种情况为尾递归。尾递归也是递归的一种特殊情形。尾递归是一种特殊的尾调用，即在尾部直接调用自身的递归函数。对尾递归的优化也是关注尾调用的主要原因。尾调用不一定是递归调用，但是尾递归特别有用，也比较容易实现。

这样的定义可能有些抽象，我们以上面的递归为例，尾递归可以写成：

def tailFib(n, prev, current):
    if n <= 1:
        return prev
    else:
        return tailFib(n - 1, current, prev + current)

也就是说，我们把需要计算的值设置为函数的参数，并通过参数传递给下一个递归函数。

需要注意的是，尾递归只是一种写法，真实的优化是编译器完成的

但对于 Java 与 Python 而言，这样是没有啥作用的……因为这两个语言并不做尾递归优化，他们相比于优化更倾向于让程序员知道 bug 的位置：在抛出异常时有完整的 Stack Trace。

但 C/C++ 不同，我们可以通过查看栈的层数来检查编译器是否进行了尾递归优化：

int tailFib(int n, int prev,int current){
    if(n <= 1)
        return prev;
    else
        return tailFib(n - 1, current, prev + current);
}

我们编写测试代码进行测试：

int tailFib(int n, int prev,int current){
    if(n <= 1)
        return prev;
    else
        return tailFib(n - 1, current, prev + current);
}
int main(void){
    int ans = tailFib(3, 1, 1);
    cout<<ans<<endl;
    return 0;
}

• 首先，我们在 -O1 的优化条件下进行测试：

  

  随后在 gdb 下测试递归三次时的栈信息：

  

  可以发现，编译器并未对尾递归进行优化。

• 随后，我们在 -O3 的优化条件下进行测试：

  

  

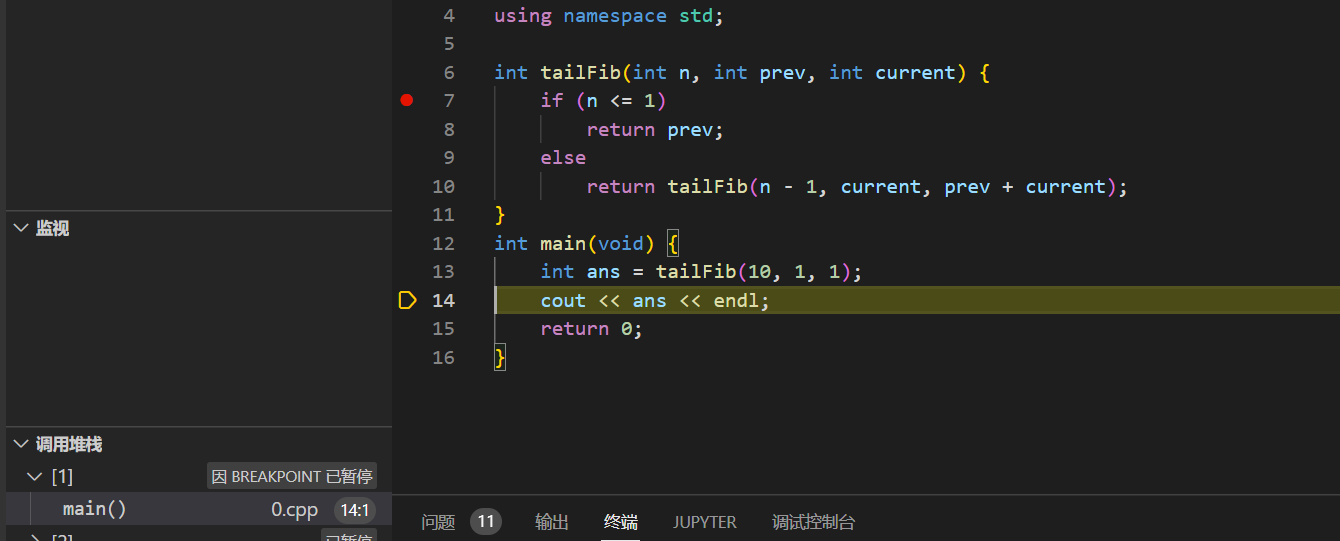
  可以发现，即使调用了10次，但始终都只有一层栈（main函数）

# 尾递归写法

啊这个真的需要讲吗

只需要在函数的尾部调用自身或者调用此函数中调用的函数即可，但不可在函数最后出现运算，如：

return tailFib(n - 1, current, prev + current) + prev;

并不能算尾递归。