一个老生常谈的话题,似乎每次学习都是从这个地方开始的(而且没继续深入过)。但是线性回归是一个很重要的内容,在谈线性回归之前,我想写解释一下什么是回归。
# 回归与分类
机器学习的任务有三种,回归,分类与聚类。我们暂且不管聚类(后面会提到),对于回归与分类,这两个任务的区别在哪?
这样说可能有些抽象,我们举一个实际的例子:预测房价。
Description
给你一堆关于 房子面积, 房子楼层, 房子区域 等等等等的数值化后的数据,想要你解决两个问题:
- 给你任意的关于一个房子的数据,判断这个房子属于什么类型的(学区房还是其他的各种类型)
- 给你任意的关于一个房子的数据,判断这个房子的价格是多少
显然,第一个问题是一个典型的分类问题,第二个是典型的回归。
那么他们的区别在哪?
仔细想想可以发现,两种问题的输入是完全一样的,模型可能用的也差不多,那么问题就出在输出上面了。
我们知道分类的输出一定是 当前这个样本属于的类别 ,而类别我们通常使用 $1, 2, 3,\dots$ 这种离散的数据来表示。但回归的输出一定是连续的数据,房子的价格不会是离散的数据。因此,回归和分类的区别就在输出是否为离散值上。
# 线性回归
通俗来说,回归就是预测输入变量与输出变量之间的关系,等价于函数的拟合。线性回归是回归中的一个特殊的问题,意味着输入变量与输出变量之间存在线性关系。形式化的说法就是: $$ y = f(x) = b + w^Tx $$ 其中 $y, b$ 为实数值,$w, x$ 为向量
我们的任务,就是使用给定的 $x$ 与 $y$ 来计算出模型中的 $w$ 与 $b$ 。如此,对于后续任意给定的 $x$ ,我们都能够预测出其对应的 $y$ 是什么。
# 参数的计算方法
那么,如何计算出 $w, b$ 呢?
我们知道,我们通过一个 $Loss$ 函数来评价模型的好坏, $Loss$ 函数值越小,则模型在训练集上表现越好。因此,如何定义 $Loss$ 函数就是我们如何计算 $w, b$ 的关键。
一般而言,我们定义 $Loss$ 函数为: $$ Loss(w, b) = \frac{1}{2N} \sum^N_{i=1}(f(x_i) - y_i)^2 = \frac{1}{2N} \sum^N_{i=1}(b + w^Tx_i - y_i)^2 $$
其中,$y_i$ 为数据真实值
我们可以发现 $(b + w^Tx_i - y_i)^2$ 的含义就是估计值到真实值之间竖直距离的平方。显然这样的 $Loss$ 定义可以衡量模型的拟合程度:$Loss$ 值越小,说明估计值与真实值之间差距越小,说明模型的表现越好。因此,当 $Loss$ 取最小值时模型的表现是最好的,这个时候我们可以找到: $$ w^, b^ = \mathop{\arg\min}\limits_{w, b}\ Loss(w, b) $$ 于是问题就转变成,如何求出 $Loss$ 函数的最小值
# 梯度下降
我们使用迭代法来求解最小值(因为很多函数不一定有解析解)。
我们知道,函数在某一点的梯度是其变化率最快的方向,但这个方向应当如何选择,才能保证我们每次走的都是往最小值的方向走的呢?
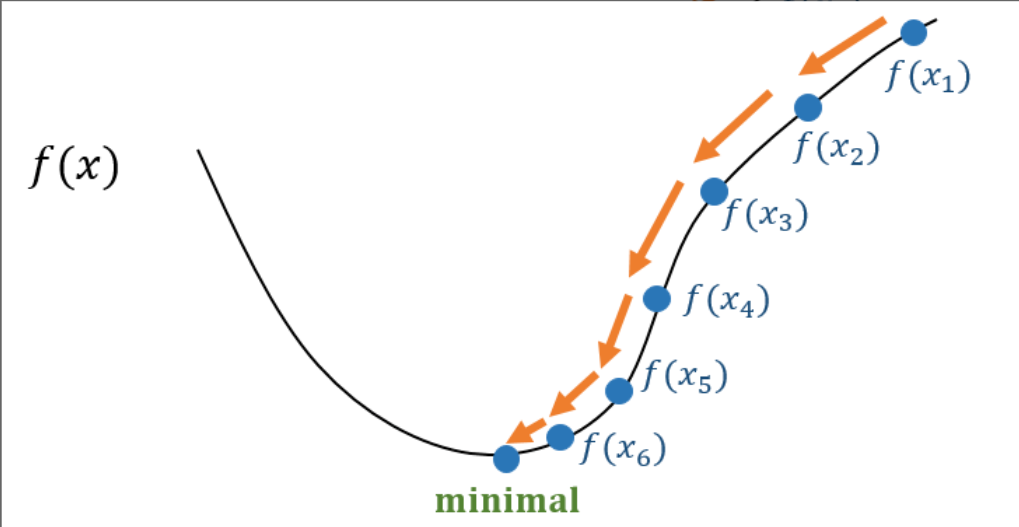
我们不妨假设 $f(x)$ 的形状是这样的,那么对于每一点的梯度,显然我们只有两个方向,$\Delta x > 0$ 或者 $\Delta x < 0$,那我们应该如何选择?
根据泰勒公式: $$ f(x + \Delta x) \sim f(x) + \Delta x\times \nabla f(x) $$ 左边是 $f(x)$ 移动一小步 $\Delta x$ 后得到的下一个点的函数值,左右两边近似相等,我们期望: $$ f(x + \Delta x) < f(x) $$ 那么我们就需要保证: $$ \Delta x \times \nabla f(x) < 0 $$ 因此,我们取 $\Delta x = -\alpha \nabla f(x), (\alpha>0)$
从而保证了 $$ \Delta x \times \nabla f(x) = -\alpha (\nabla f(x))^2 < 0 $$ 那么我们就有:$f(x + \Delta x) = f(x - \alpha \nabla f(x))$
也就是说,我们每次需要移动的一小步,就是 $-\alpha \nabla f(x)$
这样就得到了我们的梯度下降算法:
我们假设迭代函数为 $f(x)$ ,当前为第 $i$ 次迭代,此时处于 $x_i$ 点,于是我们遵循如下规则进行下一次迭代:
- 计算当前点位函数的梯度 $\nabla f(x_i)$
- 令 $x_{i +1} = x_i - \alpha \nabla f(x_i)$
直到 $\nabla f(x) \to 0$ 时停止迭代,此时我们认为找到了最小值。
其中,$\alpha$ 是一个超参数(Hyperparameter),指在机器学习任务中需要人为设定的调优参数。$\alpha$ 我们称之为 学习率,我们通常会设置学习率为$0.001$在左右,这个参数对算法的影响我们在后面会详细介绍。
# 线性回归任务
于是,我们通过梯度下降最终能够求得 $w^, b^$,进而就能够求得模型 $f(x) = b^* + w^{*T}x$,我们可以手算一个例子:
| $x_1$ | $x_2$ | $y$ |
|---|---|---|
| 1 | 1 | 3 |
| 2 | 1 | 5 |
| 3 | 4 | 8 |
我们假设模型为 $f(x) = b + w^Tx$, 其中 $x = (x_1, x_2)$
那么构造 $Loss(w, b) = \frac{1}{2 * 3}\sum^3_{i=1}(b + w^Tx_i - y_i)^2$
于是
$$
\begin{aligned}
\nabla Loss &=\left(\frac{\partial Loss}{\partial w}, \frac{\partial Loss}{\partial b}\right)\
&= (\frac{1}{3}\sum^3_{i=1}x_i(b + w^Tx_i - y_i), \frac{1}{3}\sum^3_{i=1}(b+w^Tx_i - y_i))
\end{aligned}
$$
我们将第 $i$ 次迭代时的 $w, b$ 记为 $w^{(i)}, b^{(i)}$,并假设第一次迭代时,$w^{(1)} = 0, b^{(1)} = 0$, $\alpha = 1$
于是我们有: $$ (w^{(2)}, b^{(2)}) \leftarrow (w^{(1)}, b^{(1)}) - \alpha \nabla Loss(w^{(1)}, b^{(1)}) $$ $$ (w^{(2)}, b^{(2)}) \leftarrow (0, 0) - (\frac{1}{3}\sum^3_{i=1}x_i(- y_i), \frac{1}{3}\sum^3_{i=1}(- y_i)) $$
$$ (w^{(2)}, b^{(2)}) \leftarrow ((-\frac{37}{3},-\frac{40}{3}), -\frac{16}{3}) $$ 如此反复迭代,直到 $Loss$ 值收敛不变 / $\nabla Loss = 0$ / 达到最大迭代次数
# 非线性回归
这里介绍一种较为简单的非线性回归——多项式回归
如下图所示:
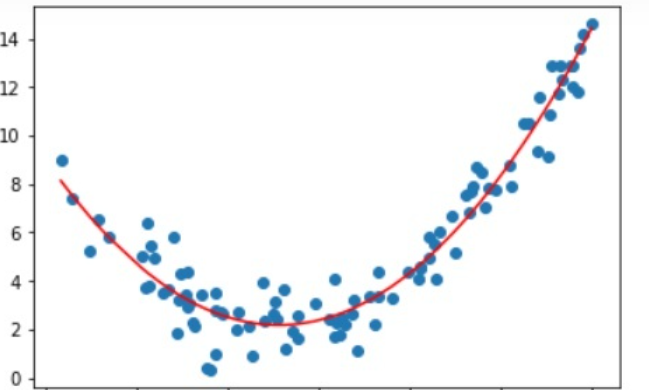
类似这样的数据,我们无法通过类似 $f(x) = b + w^Tx$ 这种线性函数来得到一个较好的拟合(显然这种模型是直线而不是这种形状的曲线)。因此这个时候我们需要多项式回归。
# 升维
如上图的曲线,从肉眼来看,大概率是一个二次曲线,那么我们应该假设模型为 $f(x) = ax^2 + bx + c$。
类似的,对于更加复杂的图像,可能二次曲线也不能描述,那么我们就会继续升维,构造 $f(x) = b + \sum^m_{i=1}w_ix^i$ ,这样的模型就被称之为多项式回归。
然而,多项式回归也可以转化成线性回归的形式: 我们可以构造一个线性映射 $T$ ,$T$ 是从 $\mathbb{R}^m$ 到 $\mathcal{P}_m$ 的线性映射,其中 $\mathcal{P}_m$ 是一个线性空间,其标准基为 $(1, x, x^2,\dots, x^m)$
我们构造的映射 $T$ 具体而言:
$T$ 使得 $z_1 = x, z_2 = x^2, z_3 = x^3, \dots, z_m = x^m$
如此,$f(x) = b + \sum^m_{i=1}w_ix^i = b + \sum^m_{i=1}w_iz_i = b + w^Tz$,我们就得到了上面线性回归的式子,也就意味着,我们可以用线性回归的方法来做多项式回归了。
easy
# 过拟合与欠拟合
在多项式回归中,这两个是经常遇见的问题。原因在于,我们事先并不知道 $m$ 是多少。
如果我们 $m$ 选取的较小,那么有可能会出现下面的情况:
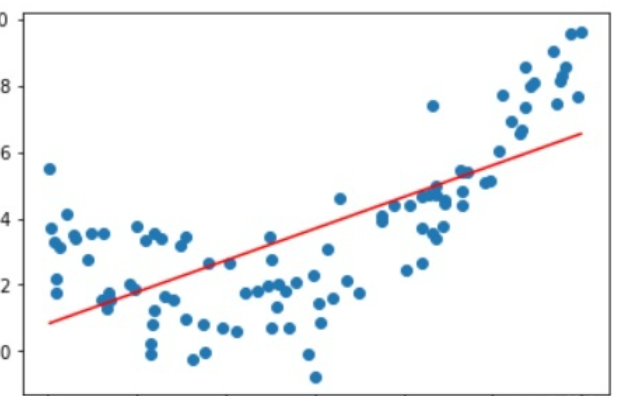
而如果我们的 $m$ 选取的很大,有可能会出现这样的情况:
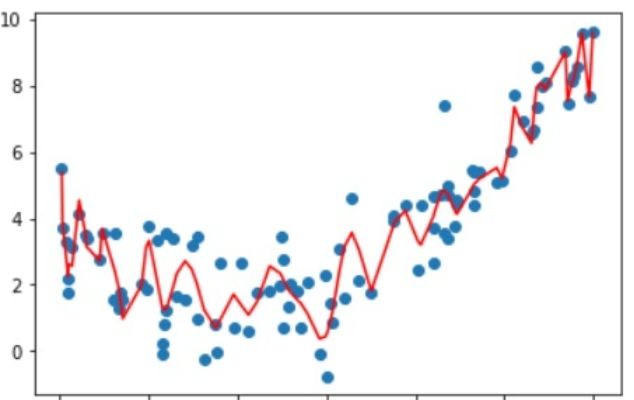
你可能会觉得,第一种情况确实拉跨,但第二种情况的表现不是很好吗?
在某种意义上,第二种模型的表现确实很好,他把数据集中所有点的特征都考虑到了,不管高的低的全部都能覆盖到。但我们知道,数据集并不是干净的,也就是说,在数据中存在 噪声点,噪声点是干扰信息,并不能很好的反映数据真实的特征,因此我们应当将其忽略。
但如果你的模型发生了过拟合,那么模型就会被噪声点干扰,从而呈现出训练集上表现很好,但测试集上表现很差的情况
那么我们如何避免这两种情况的发生呢?
欠拟合是显然的,我们只需要升维!升维!或者说,我们只需要把增加训练次数,增加模型的复杂程度即可。
在机器学习任务中,主要解决的都是过拟合问题。因为我们希望,我们的模型不仅仅是在训练集上跑得好,我们希望他在测试集,验证集,甚至是实际应用中都能够有不错的成绩(这种能力被称为泛化能力)
那么,为了解决过拟合问题,我们主要有三种方法:
更多的训练数据。有些时候过拟合可能是因为数据集太小,训练来训练去也只有那几个数据在掰扯,没有意义。所以我们可以通过增大训练集,通俗一些,就是我们可以让模型多学一点,把东西都学完,这样不管遇到什么情况,他在测试集上的表现一定不会差。
数据增强。这部分会在后面的
CNN中提到让模型更简单。在多项式回归中就是说,我们需要适当的减小 $m$。具体而言,我们将更改 $Loss$ 的定义。
我们定义 $Loss$ 函数为 $$ Loss(w, b) =\frac{1}{2N} \sum^N_{i=1}(f(x_i) - y_i)^2 + \lambda J(f) $$ 其中 $J(f)$ 为模型的复杂程度,被称为 正则化项
通过这样定义 $Loss$ 函数,我们可以将模型的复杂程度与拟合程度统筹考虑。这种类型的 $Loss$ 函数被称为结构风险最小化
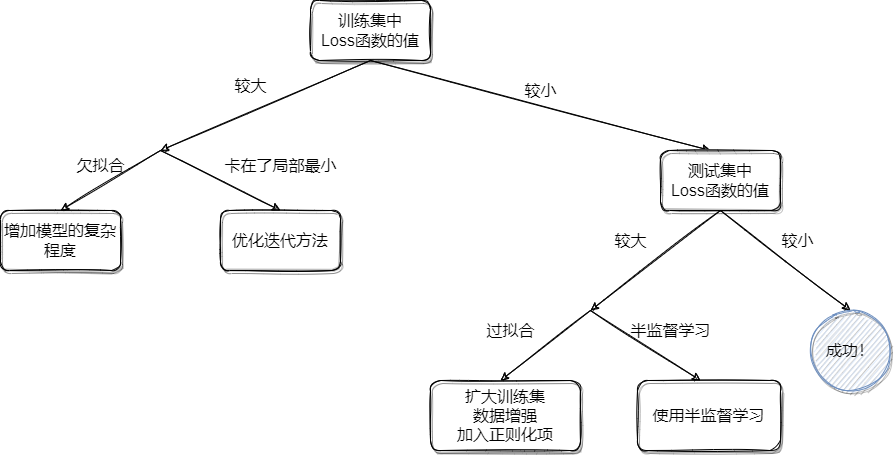
# 总结
如图: