在这里，我们重点谈谈 如果模型训练不动了怎么办

# 驻点问题

当梯度很小时，并且我们发现我们没有成功训练出一个模型的时候，也就是 $Loss$ 函数还比较大的时候：

那么我们可能遇到了两个问题：

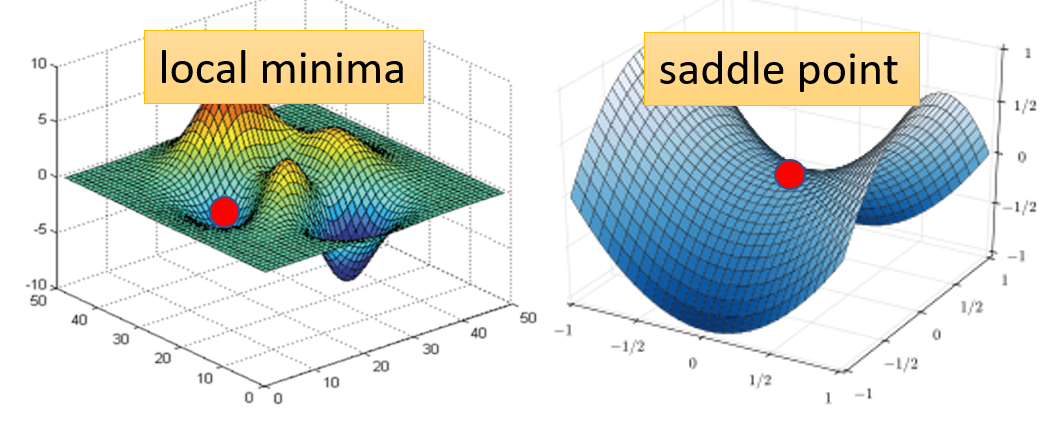
我们卡在了局部最小或是我们卡在了鞍点。像这种梯度为 $0$ 的点，我们统称为驻点(critical point)

那么，当我们发现我们的梯度非常接近 $0$，卡在了一个驻点，那么我们能不能知道我们到底是卡在了局部最小还是鞍点呢？

为什么会想要知道驻点的类型

这是因为如果我们现在处于局部最小，那么我们不一定能够跑出来（根据朴素方法），但是如果卡在了鞍点，显然我们还是可以继续下降的

这里我们需要一些数学知识：多元函数的泰勒展开。

我们将 $L(\theta)$ 在 $\theta = \theta^{\prime}$ 这一点展开： $$ L(\theta) = L(\theta^{\prime}) + (\theta - \theta^{\prime})^T\mathop{g} + \frac{1}{2}(\theta -\theta^{\prime})^T\mathop{H}(\theta - \theta^{\prime}) + o(\theta^T\theta) $$ 其中，$\mathop{g} = \nabla L(\theta^{\prime})$ 为 $L(\theta)$ 在 $\theta = \theta^{\prime}$ 处的梯度，$\mathop{H}$ 称为海森矩阵(Hessian Matrix)，$H_{ij} = \frac{\partial^2}{\partial\theta_i\partial\theta_j}L(\theta^{\prime})$

那么由于我们现在到了一个驻点，于是 $g = \nabla L(\theta^{\prime}) = 0$

那么我们就有 $$ L(\theta) = L(\theta^{\prime}) + \frac{1}{2}(\theta -\theta^{\prime})^T\mathop{H}(\theta - \theta^{\prime}) + o(\theta^T\theta) $$ 因此，我们只能借助 $\frac{1}{2}(\theta -\theta^{\prime})^T\mathop{H}(\theta - \theta^{\prime})$ 这个二次型来判断 $\theta^{\prime}$ 是什么类型的点了。

我们移项后，分三种情况考虑：： $$ L(\theta) - L(\theta^{\prime}) = \frac{1}{2}(\theta -\theta^{\prime})^T\mathop{H}(\theta - \theta^{\prime}) = \begin{cases}

0\ < 0\ Sometimes > 0, sometimes < 0 \end{cases} $$ 于是，可以得出结论：

1. 当 $H > 0$ 时，$\theta^{\prime}$ 为极小值点
2. 当 $H < 0$ 时，$\theta^{\prime}$ 为极大值点
3. 若 $H$ 至少有一个特征值大于0，且至少有一个特征值小于0，则 $\theta^{\prime}$ 为鞍点

当我们判定，一个点是鞍点时，不需要害怕，因为你完全可以跑出鞍点：

我们只需要对 $H$ 进行分解，得到特征值与对应的特征向量，随后，我们朝着特征值为负的特征向量方向更新参数即可。

负的特征值代表这个值对于那个曲面而言是应该极大值点

# 局部最小点与鞍点

这两种点之间有着不得不说的关系。

我们以一个二维图像为例：

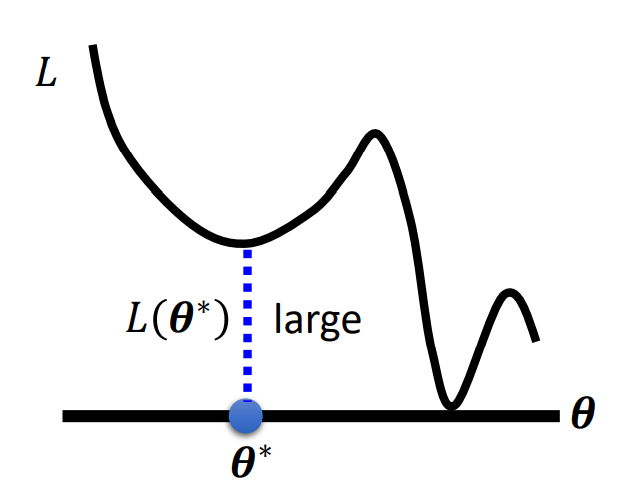
我们发现模型现在似乎卡在了一个局部最小的位置，但，真的是这样吗？

如果我们升高一个维度来看，可能这个局部最小会是这样的：

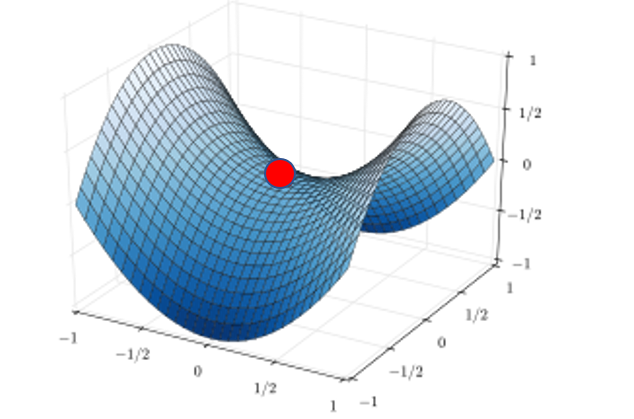
也就是说，在低维空间下看到的一个局部最小，在高位空间看起来它可能就是一个鞍点而已，如果是鞍点的话，我们就有办法可以快速的逃脱。

而在训练模型的过程中，我们会经常遇到梯度很小的情况：

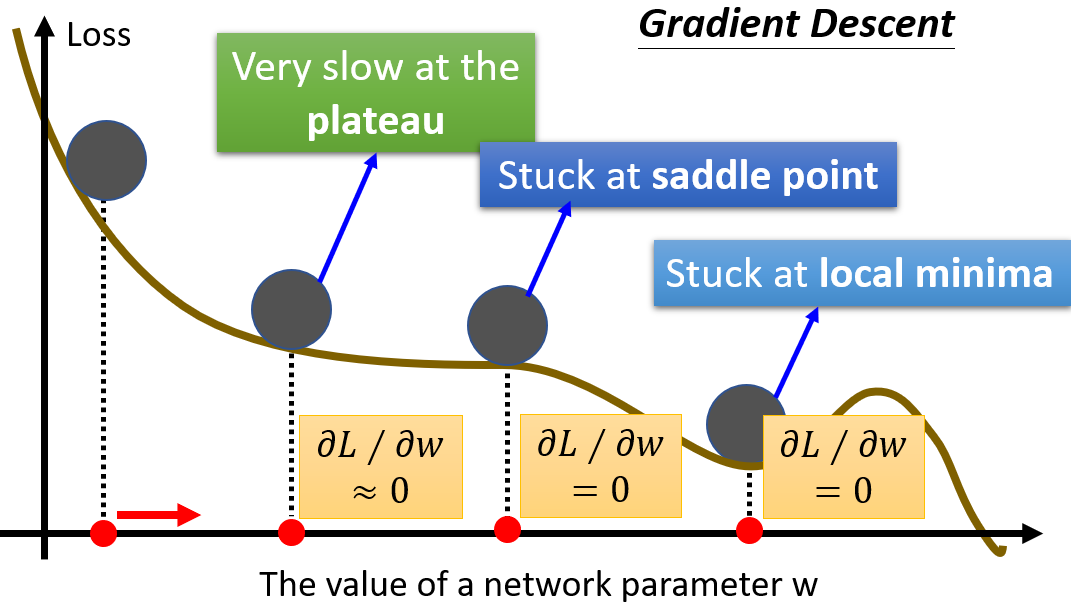
在这种条件下，由于我们的 $\alpha$ 是确定的，所以如果使用朴素的梯度下降，我们在卡在驻点时很难逃脱，因此我们给出两种解决方法：

1. 随机梯度下降（SGD）
2. 动量（Momentum）

# 随机梯度下降(Stochastic Gradient Descent)

在讲 SGD 之前，我们需要补充一下 Batch Gradient Descent，批量梯度下降的定义。

批量梯度下降，名头看起来很大，其实本质上就是最朴素的梯度下降。在前面一篇中我们提到，我们每次更新参数的公式为： $$ \begin{aligned} (w^{(i+1)}, b^{(i+1)}) &= (w^{(i)}, b^{(i)}) - \alpha\nabla Loss(w^{(i)}, b^{(i)}) \ &= (w^{(i)}, b^{(i)}) - \alpha(\frac{\partial Loss}{\partial w}, \frac{\partial Loss}{\partial b})\ &= (w^{(i)}, b^{(i)}) - \alpha(\frac{1}{N}\sum^N_{j=1}x_j(b^{(i)} + w^{(i)T}x_j - y_j), \frac{1}{N}\sum^N_{j=1}(b^{(i)}+w^{(i)T}x_j - y_j)) \end{aligned} $$

我们将整个样本当做一个批次(batch)，每完成一次参数更新（即完成一次训练），我们成为完成了一次 epoch。

这种方法的优点是迭代次数很少，一般来说可能迭代 10000 次就能够有着较好的效果，但会遇到很多问题诸如：

1. 需要的时间太长，因为我们每次都要看遍数据集，当数据集很大的时候是非常费劲的
2. 计算量很大，就像我们这里使用的 MSE 一样，计算量非常大，还有可能导致数据溢出的情况（ MSE 算到 1e100 不是什么难事）
3. 每次的参数更新都在遍历完数据后，但有些例子可能是对参数更新无用的，我们无法分辨出来

我觉得主要是时间上来说无法接受，机器学习可能还好一些，深度学习领域中数据集都特别大，像这种训练一次要看几百万条数据的肯定寄了

因此我们引入了 SGD 算法。

随机梯度下降的做法是在每次迭代时随机选取一个样本来对参数进行更新，具体而言：

我们假设损失函数还是 MSE ，于是我们计算 $\nabla Loss$ （注意，我们每次只选取了一个样本，比如我们这里选择样本 $j$ ） $$ \nabla Loss_j = (x_j(b^{(i)} + w^{(i)T}x_j - y_j), (b^{(i)}+w^{(i)T}x_j - y_j)) $$ 于是我们的参数更新公式为： $$ (w^{(i+1)}, b^{(i+1)}) \leftarrow (w^{(i)}, b^{(i)}) - \alpha \nabla Loss_j $$ 这样做的优点是很显然的，我们每次只随机看了一个数据的梯度，然后根据这个梯度来更新参数，这样我们每一轮训练的速度都大大加快，从 $O(m)$ 直降为 $O(1)$ ，并且使用 SGD 是有几率跳出局部最小这个坑的，可以这样理解，每次针对单个数据样例进行摸索前进时，本质上是在一个样例形成的误差曲面上摸索前进，而每个样例的曲面大体类似，又不尽相同，当你掉入一个坑里时，往往能被别的曲面拽出来。

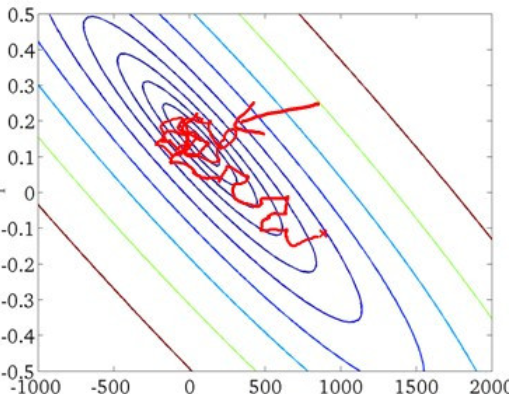
但缺点同样明显，随机嘛，你也不知道你这个梯度会不会收敛，他可能在最小值附加波动，也可能你训练了一万轮都没找到最小值，因此SGD 需要的迭代次数较多，并且如果我们查看 SGD 的解空间的话（就是把每次的参数 $w, b$ 列出来画个图），我们 SGD 的搜索过程大多数比较盲目，如果说批量梯度下降是一条贪吃蛇，那 SGD 就是一条打了许多结的麻绳（

可以看看这个图，领略一下 SGD 找最优解的过程

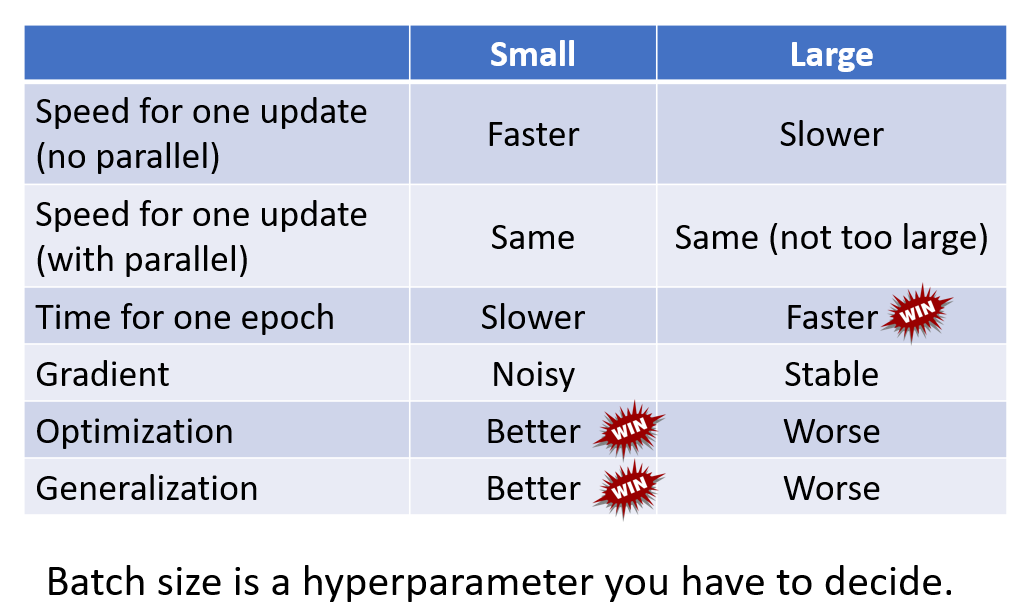
# Mini-batch Gradient Descent (SGD + Batch)

我们想，我们能不能找到一种折中的方法，既能保留 SGD 的速度，又能保持 BGD 的有目的的寻找呢？

我们可以将 SGD 视为一种另类的 BGD：事实上，我们只是把 batch-size 设置为 $1$ ，这样每一条数据都是一个 batch，然后我们每次训练都随机选择一个批次，对参数进行更新。

那么这就给了我们一种启发：如果我们每次的 batch-size 选为一个特定的值（这个值一般而言比较小，是一个超参数，一般会选择几百以内），每次都随机选择一个 batch 进行迭代，这样我们既能保持了 SGD 的高速度，又不至于有 SGD 的那些困扰。

算法的过程可以描述为：

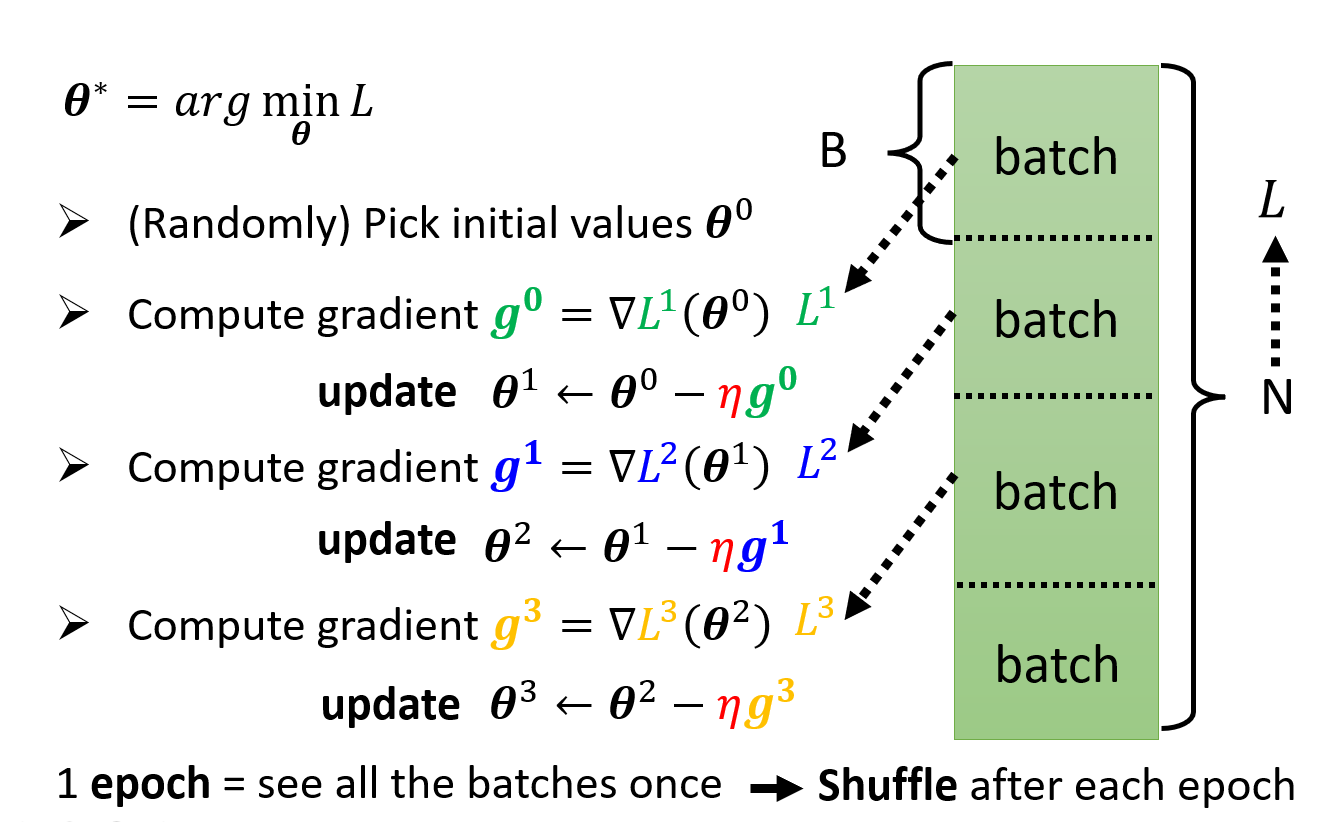
在这里有一个拓展，就是 batch-size 的选择对于优化的影响是非线性的，关于这点可以自己去看看，我这里放一张图。

# 动量

这个优化方法很有意思，我们把参数优化的过程想成是一个球沿着函数曲线滚动的过程。如果我们把这个球从最高处释放，他会怎么动呢？（不要考虑摩擦！）

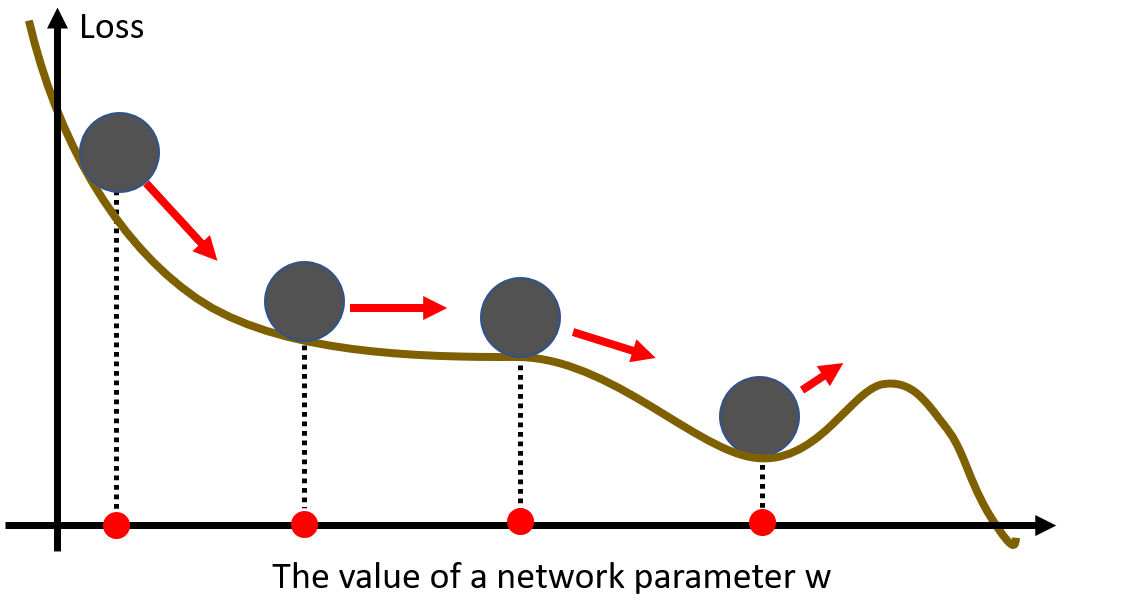
显然，在最后这个地方，如果他的 “速度” 足够的话，是能够冲上去的，也就是说它能不被一个局部最小卡住（前提是速度足够）

在这里，我们将其称之为 “动量”，（事实上也确实是动量），我们如果每次更新参数的时候能够把这个动量考虑进去的话，那么我们岂不是就能够不被局部最小困扰了？

但问题在于应该怎么加进来。

我们看原始的梯度下降的运动合成（毕竟是向量嘛，可以这么玩）：

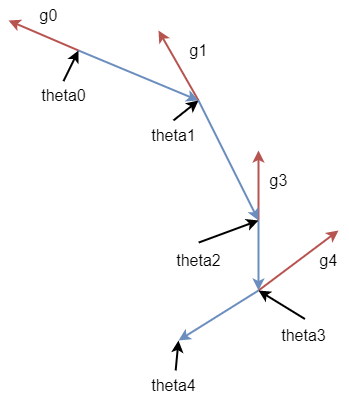
如果我们引入一个动量 $m$ 的话，这个时候的运动合成就变成了：

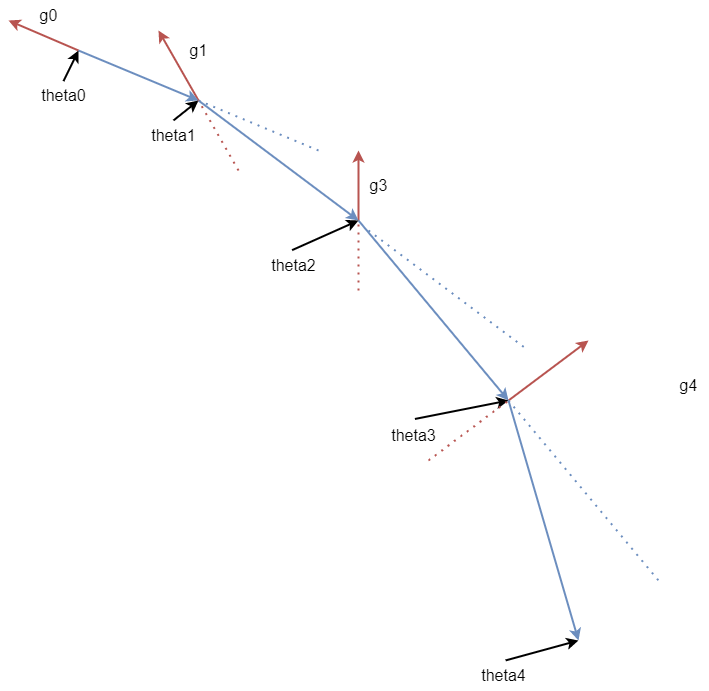
事实上，我们的做法是将参数更新的公式进行了更改： $$ \theta^{(0)}, m^{(0)} = 0 $$

$$ m^{(i+1)} = \lambda m^{(i)} - \alpha \nabla Loss(\theta^{(i)}) $$

$$ \theta^{(i+1)} = \theta^{(i)} + m^{(i+1)} $$ 这样而言，我们每次计算的 $m$ 事实上都是前面我们走过的梯度的合成，也就是我们的初速度（），这样即使我们当前的梯度是个负值（梯度为负的话就说明梯度在把你往后拉），但我们的动量是个正值，这样我们就不会轻易被梯度给拉回去（拉回一个局部最小）

这个想法我第一次看见的时候确实比较震撼，因为我觉得可能批次梯度下降已经够好了，虽然还是不太能完全解决局部最小的问题。但这个算法在很大程度上确实能够逃出局部最小（虽然也存在逃不出去的情况，这也很常见）

# 自适应学习率

在上面我们讲了驻点问题与解决方法，但其实驻点可能并不一定是训练一个模型时遇到的最困难的问题……

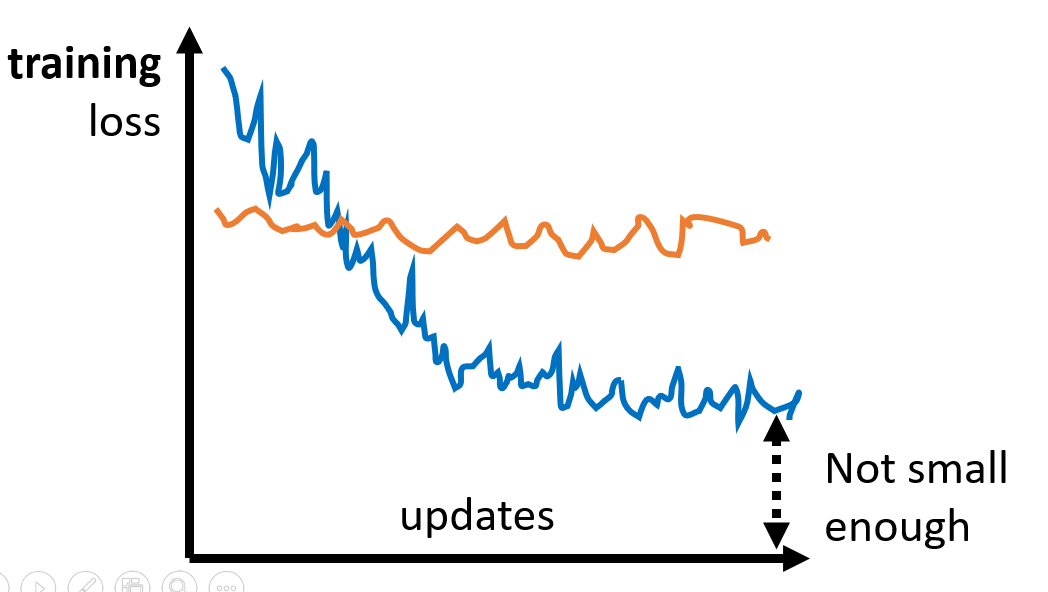
我们模型训练不起来有时候可能不一定是遇到了驻点，而是……我们更新参数时开始了反复横跳。如下图：

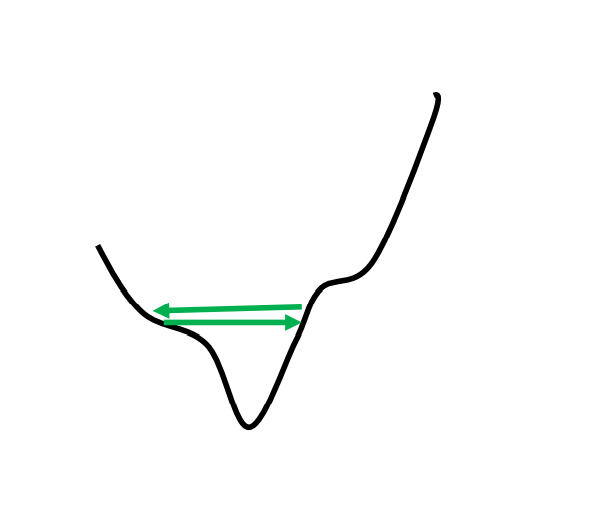
那为什么会出现这个问题呢？你看它梯度下降的方向也没问题（参数更新的方向没错），但是为什么就是下不去呢？

这里就要提到我们第一个接触的超参数——学习率 $\alpha$ 。我们知道 $\alpha$ 决定了你下一步应该走多远，这个超参数的设定是较难的，如果设定大了，可能就会出现上面这种情况，如果小了，那收敛的速度又太慢，一个小数据集算个几分钟出不来结果（基本是寄了的）

可以看看这两张图：

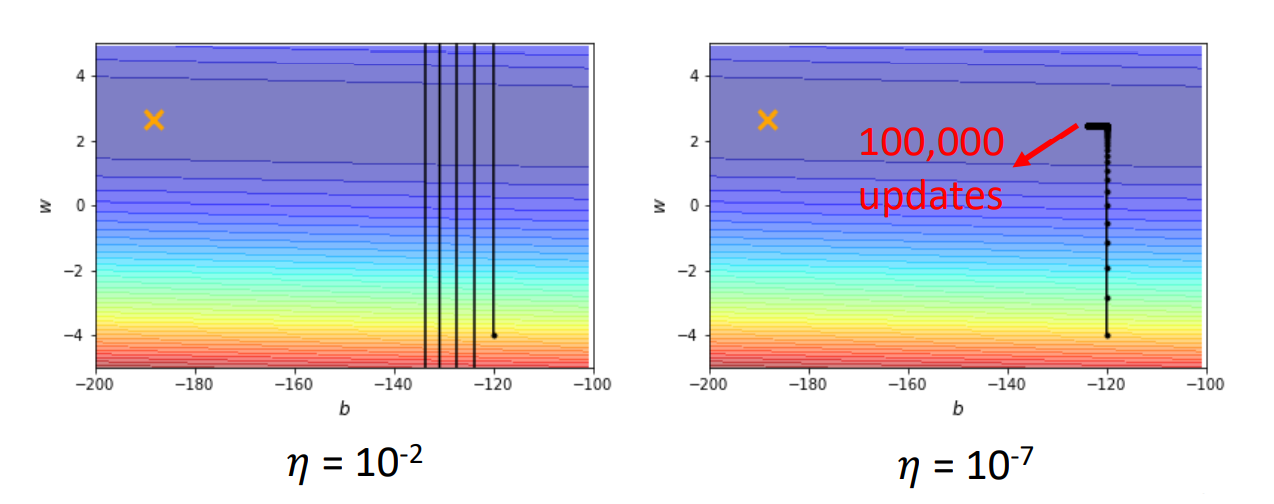
所以，我们想，能不能设计一种算法，让这个学习率可以自动调整呢？这样我们只需要给一个差不多的初值就行了

懒人改变世界（bushi

古圣先贤也这么想，所以他们陆续提出了一些算法，我按照发展的流程来一一解释。

# Adagrad

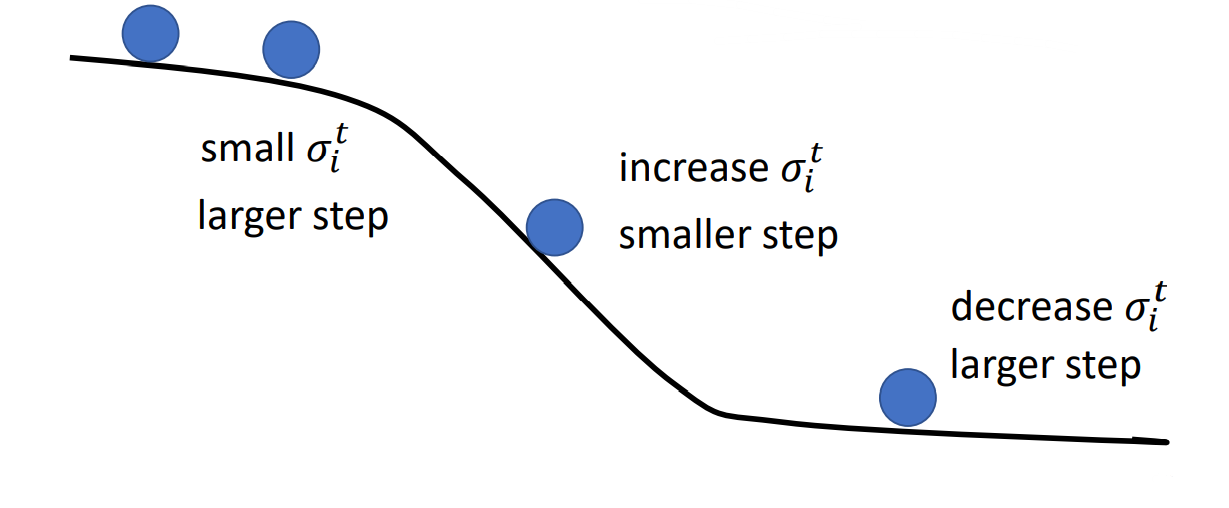
这是最早被提出的方法，它的想法是说：如果在某一个方向上函数的梯度很小（也就是说在这个方向上函数很平坦），那么我们期望有较大的学习率，否则我们需要一个较小的学习率。

那么我们的参数更新就写为： $$ \theta^{(i+1)} = \theta^{(i)} - \frac{\alpha}{\sigma^{(i)}}\nabla Loss(\theta^{(i)}) $$ 也就是说我们在原来 $\alpha$ 的基础上增加了一个随着迭代次数变化的分母 $\sigma^{(i)}$，那么这个 $\sigma^{(i)}$ 应该如何变化呢？

如下所示： $$ \theta^{(1)} = \theta^{(0)} - \frac{\alpha}{\sigma^{(0)}}\nabla Loss(\theta^{(0)})\quad \sigma^{(0)} = \sqrt{(\nabla Loss(\theta^{(0)}))^2} = ||\nabla Loss(\theta^{(0)})||_2 $$

$$ \theta^{(2)} = \theta^{(1)} - \frac{\alpha}{\sigma^{(1)}}\nabla Loss(\theta^{(1)})\quad \sigma^{(1)} = \sqrt{\frac{1}{2}(\nabla Loss(\theta^{(0)}))^2 + \nabla Loss(\theta^{(1)}))^2)} $$

$$ \vdots $$

$$ \theta^{(i+1)} = \theta^{(i)} - \frac{\alpha}{\sigma^{(i)}}\nabla Loss(\theta^{(i)})\quad \sigma^{(i)} = \sqrt{\frac{1}{i+1}\sum^i_{j=1}\nabla Loss(\theta^{(j)})^2} $$ 也就是说，我们的这个 $\sigma$ 事实上是一个梯度的均方根。

那么这样的作用到底是什么呢？

Adagrad 起到的效果是在参数空间更为平缓的方向，会取得更大的进步（因为平缓，所以历史梯度平方和较小，对应学习下降的幅度较小），并且能够使得陡峭的方向变得平缓，从而加快训练速度。

但缺点十分明显，由于我们会记录历史中所有梯度的平方和，因此，学习越深入，更新的幅度就会越小。换个说法就是，当训练的次数增多的时候，我们的学习率会衰减的非常快，甚至变成0。

为了改善这个问题，提出了 RMSProp 算法。

# RMSProp

RMSProp 对 Adagrad 的算法进行了一些修改，让我们的学习率不至于衰减的如此之快。如下所示： $$ \theta^{(1)} = \theta^{(0)} - \frac{\alpha}{\sigma^{(0)}}\nabla Loss(\theta^{(0)})\quad \sigma^{(0)} = \sqrt{(\nabla Loss(\theta^{(0)}))^2} = ||\nabla Loss(\theta^{(0)})||_2 $$

$$ \theta^{(2)} = \theta^{(1)} - \frac{\alpha}{\sigma^{(1)}}\nabla Loss(\theta^{(1)})\quad \sigma^{(1)} = \sqrt{\beta(\sigma^{(0)})^2 + (1-\beta)(\nabla Loss(\theta^{(1)}))^2} $$

$$ \vdots $$

$$ \theta^{(i+1)} = \theta^{(i)} - \frac{\alpha}{\sigma^{(i)}}\nabla Loss(\theta^{(i)})\quad \sigma^{(i)} = \sqrt{\beta(\sigma^{(i-1)})^2 + (1-\beta)(\nabla Loss(\theta^{(i)}))^2} $$ 其中 $0<\beta<1$ 。

那么这样为什么就可以延缓学习率衰减的过快呢？

你可以发现，每一个 $\sigma$ 都是由历史所有的梯度与这次的梯度算的加权和，也就是说，我们可以通过调整 $\beta$ 来让最近的梯度有着更高的影响力，让很早之前的梯度影响降低甚至为 $0$

就像这样：

但是啊，这种学习率自适应算法没办法解决我们之前说的卡在驻点的情况，那么有没有一种算法可以统筹解决这两个问题呢？

于是我们就有了 Adam 算法

# Adam

Adam 就是 RMSProp + Momentum

具体而言，我们的参数更新就变成了： $$ g^{(i+1)} = \nabla Loss(\theta^{(i)}_j) $$

$$ m^{(i+1)} = \beta_1m^{(i)} + (1-\beta_1)g^{(i+1)} $$

$$ \sigma^{(i+1)} = \beta_2 \sigma^{(i)} + (1-\beta_2)(g^{(i+1)})^2 $$

$$ \hat{m}^{(i+1)} = \frac{m^{(i+1)}}{1-\beta_1^{i+1}} $$

$$ \hat{\sigma}^{(i+1)} = \frac{\sigma^{(i+1)}}{1-\beta_2^{i+1}} $$

$$ \theta^{(i+1)} = \theta^{(i)} - \frac{\alpha\hat{m}^{(i+1)}}{\sqrt{\hat{\sigma}^{(i+1)}} + \epsilon} $$ 其中， $\alpha, \beta_1, \beta_2, \epsilon$ 都是超参数，一般选择 $0.001, 0.9, 0.999, 10^{-8}$（原始论文中是这么选择的）

那 Adam 好在什么地方呢？

我们可以看，如果只用动量，我们会遇到这样的情况：

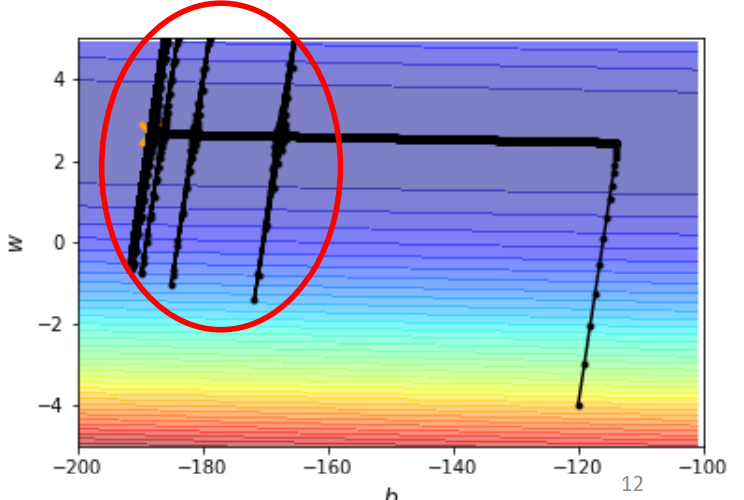
如果只用 RMSProp 的话，显然我们也会遇到学习率衰减的问题，这样在梯度也很小的时候，我们也会卡在一个驻点没办法逃离。

使用 Adam 的话，我们就可以达到这样的效果：

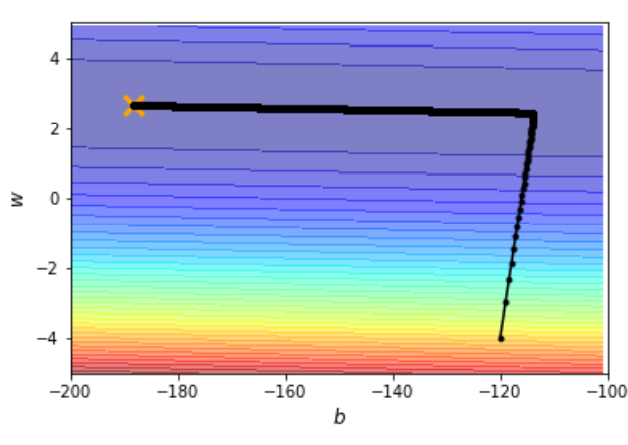
完美