Featured image of post Perceptron And Neural Networks
我的许多零零碎碎

Perceptron And Neural Networks

感知机

# 感知机

感知机(perceptron) 是一种二分类的线性分类模型，也就是说，输入数据通过模型运算后可以输出分类的类别，由于是二分类，所以类比只有 $+1, -1$

我们举个例子，如果我们的输入空间是一个二维空间的话，那么感知机实际上就是找到一条直线，这条直线能把我们输入的点完全分为两个部分，如图所示：

Case

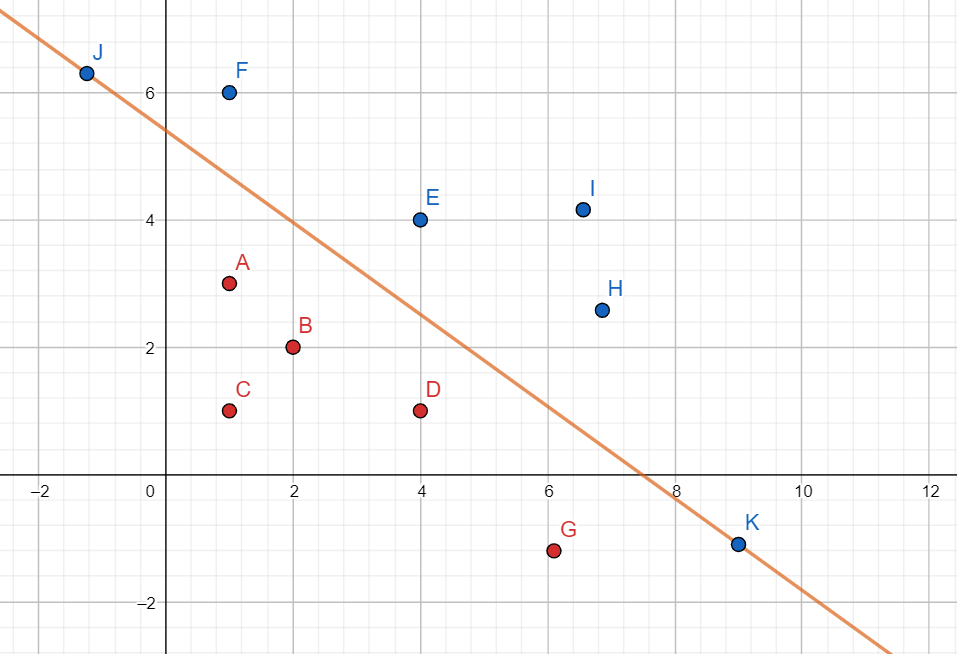
这条直线就是感知机做的事情，下面这些红色的点，感知机将其打上标签为 $-1$ ，上面这些蓝色的点，感知机打上标签为 $+1$

标签我们可以当做是这些点的颜色，不需要觉得这是另一个维度

在更高维度的输入空间中，感知机所做的就是 找到一个分离超平面，可以把输入空间内的点划分为正负两类

# 感知机模型

我们给出数学上模型的定义： $$ f(x) = sign(b + w^Tx) $$ 这里的 $sign()$ 为符号函数： $$ sign(x) = \begin{cases} 1, x\geq 0\ -1, x < 0 \end{cases} $$ $w$ 称为权值向量， $b$ 称为偏置(bias)

我们可以发现，其实这个就是一个线性回归的模型，但是由于是分类问题，我们在这个基础上加了一个取符号的函数来满足二分类的性质而已。

感知机有如下的几何解释：线性方程 $$ w^Tx + b = 0 $$ 对应着输入空间中的一个超平面 $S$ ，其中 $w$ 是超平面的法向量，$b$ 是超平面的截距。这个超平面将输入空间分为两个部分，位于两个部分的点分别被打上正类，负类的标签。因此超平面 $S$ 称为分离超平面。

感知机的预测，就是对于新的输入实例，感知机输出其对应的类别。

# 感知机学习策略

首先，我们需要提出一个概念：线性可分性

如果对于一个数据集 $T$，我们可以找到一个超平面 $S$ 使得 $T$ 中的正实例点与负实例点完全划分到 $S$ 的两侧，那么我们称 $T$ 是线性可分的。

$T$ 可以表示为 $T = {(x_1, y_1), \dots, (x_n, y_n)}$，其中 $x_i \in \mathbb{R}^m, y_i \in {+1,-1}$

举一个例子，类似于之前的那张图，那样的数据集就是线性可分的，但如果是这样的话，就是线性不可分的：

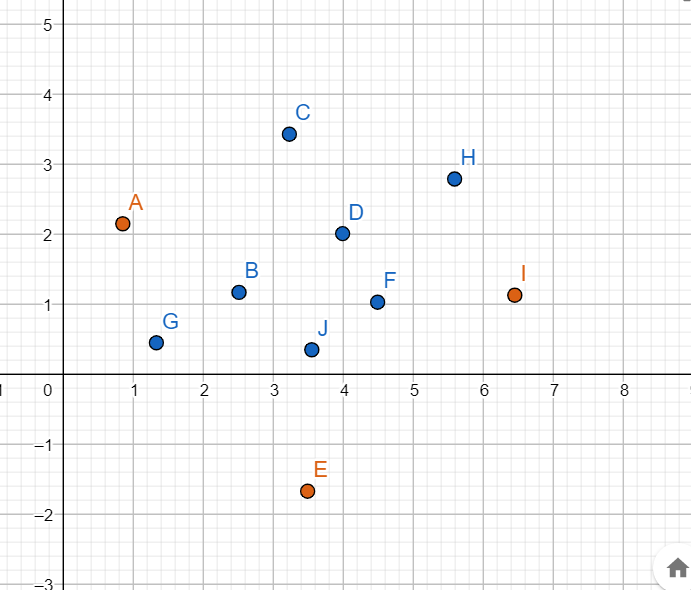
Bad Case

这种我们就没法找到一条直线，把蓝色和橙色的完全分开

现实当中线性不可分的例子占大多数

一般来说，我们假设数据集是线性可分的，那么我们目的就是寻找参数 $w, b$

但这里我们不应该使用 MSE 来解决问题了（因为 MSE 这个损失函数无法度量分类错误的损失），对于分类问题，我们最好的损失函数应该是误分点的数量，但这种损失函数不是连续可导的（数量显然是应该离散值），不易优化（即使用梯度下降来找最小值），于是我们需要想出一种能度量误分点的，又是连续可导的函数。

这里，我们构造损失函数 $Loss$ 为：误分类点到超平面 $S$ 的总距离，我们通过如下数学形式来描述：

  1. 首先，我们写出数据集中任意一点到 $S$ 的距离（就是点到直线距离） $$ \frac{1}{||w||}|w^Tx+b| $$

  2. 然后，对于误分类点 $x_i$（就比如这个点的$y_i = -1$ ，但是$sign(w^Tx_i+b) = +1$ 这种情况），我们有一个性质成立： $$ -y_i(w^Tx_i + b) > 0 $$

  3. 于是，误分类点 $x_i$ 到超平面的距离可以写成： $$ -y_i\frac{1}{||w||}(w^Tx_i+b) $$

    为什么可以这么写呢？因为你要知道 $y_i$ 只是正负一，所以我这里乘一个 $-y_i$ 只是为了保证 $w^Tx_i + b$ 这个是正的，相当于取了一个绝对值了

所以，我们就可以构造 $Loss$ 为： $$ Loss(w, b) = -\frac{1}{||w||}\sum_{x_i\in M}y_i(w^Tx_i+b) $$ 这里的 $M$ 是误分点的集合。

但我们发现，这个 $\frac{1}{||w||}$ 好像没啥用处，而且算起来还麻烦（因为你分子小的话就行了，分母小没所谓，真正度量误分点距离的分子占的比重要大一些）

所以我们真正采用的损失函数是这样的： $$ Loss(w, b) = -\sum_{x_i\in M}y_i(w^Tx_i+b) $$ 显然这个损失函数的最小值为 $0$ ，也就是没有误分点的情况，但就像我之前说的，大多数数据集都是线性不可分的，所以有时候我们只是求出一个最优超平面，如果想要准确的话，我们会在 SVM 中详细讲述。

所以感知机挺拉跨的（因为它要求数据集线性可分，这样它的训练算法才收敛，否则就寄了）

# 感知机的训练

感知机的训练采用了随机梯度下降，我们用一张图来描述它的算法，并手算一个实例来帮助理解。

首先我们知道，对 $Loss$ 求梯度得到 $\nabla Loss(w, b) = (-\sum_{x_i\in M}y_ix_i, -\sum_{x_i\in M}y_i)$，而由于我们是随机梯度下降，所以每次我们都只从 $M$ 中随机选择一个点 $x_t$ 来进行梯度下降，这样我们写作 $\nabla Loss(w, b)|_t = (-y_tx_t, -y_t)$

算法如图所示：

Algorithm

我们举一个例子：

我们有这样一个数据集，其中正实例点为 $x_1 = (3, 3), x_2 = (4, 3)$，负实例点 $x_3 = (1, 1)$，请训练一个感知机模型 $f(x) = sign(w^Tx + b)$，其中学习率 $\alpha = 1, w_0= 0, b_0 = 0$

迭代过程如下图所示：

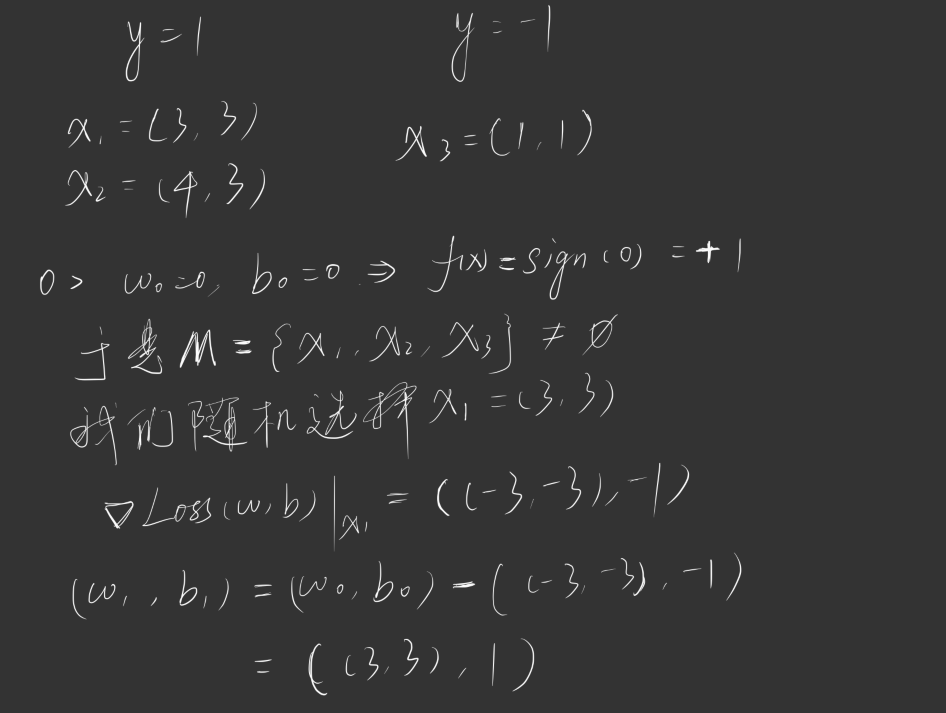
Step-1

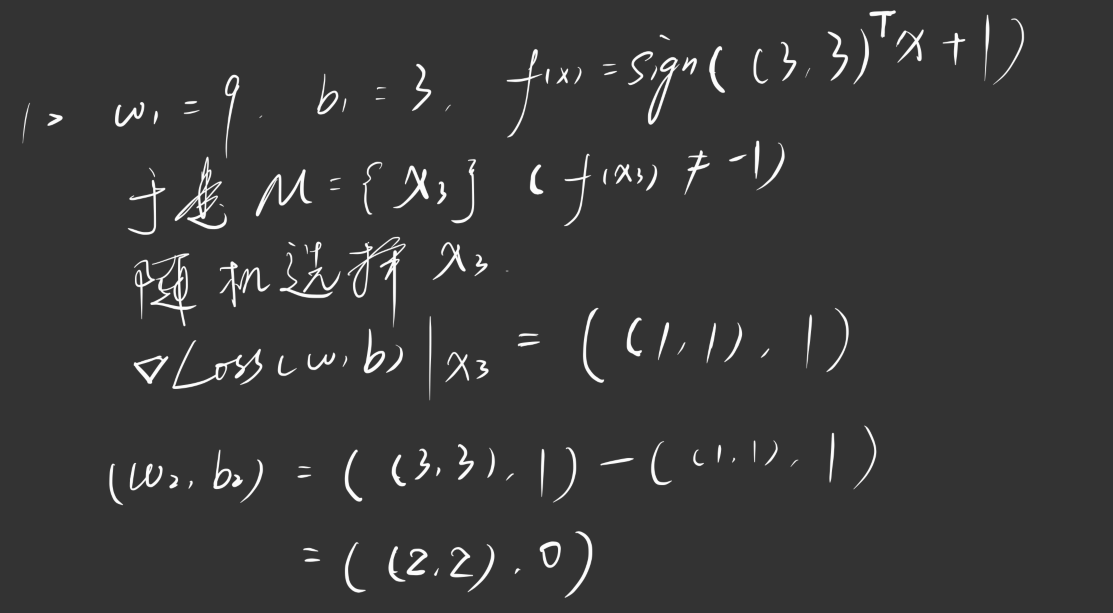
Step-2

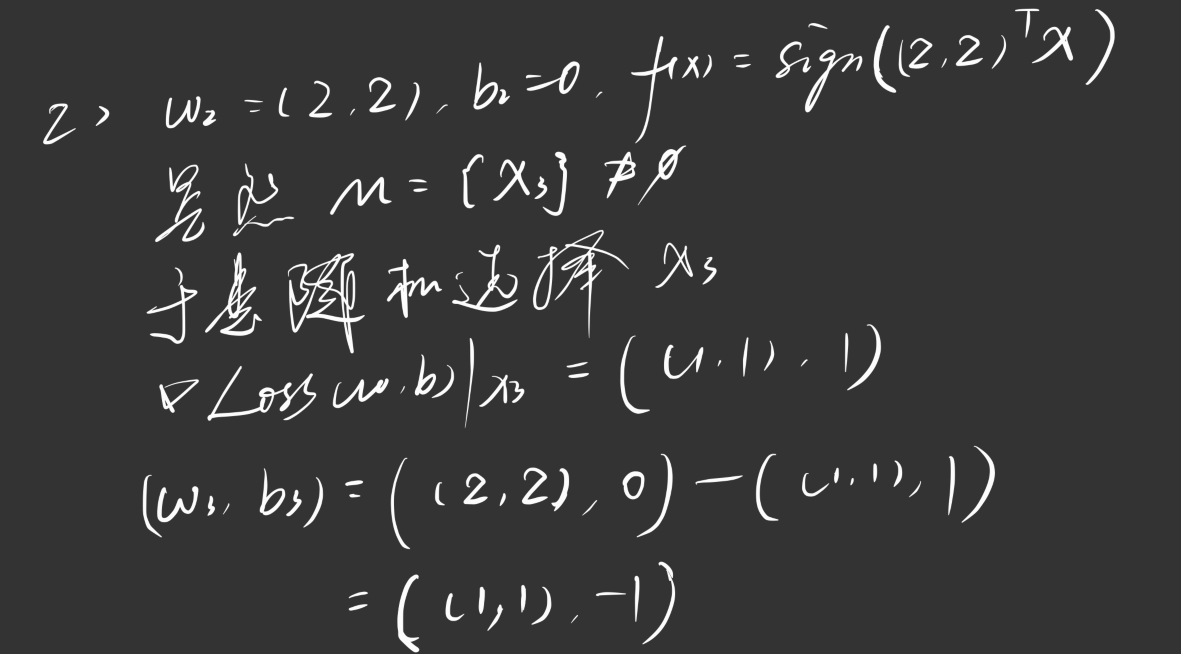
Step-3

依此类推，直到 $M$ 为空集终止迭代。

值得一提的是，这个分离超平面不是唯一的，会随着我们每次随机选择的不同样本而计算出不同的分离超平面（与 SVM 不同），我这里算出来的是 $f(x) = sign((1, 1)^Tx - 3)$

# 神经网络

来到了一个很熟悉的名词，但你可能并不真的知道这到底是什么。

我们先来看刚刚说的感知机，事实上我们可以把感知机图形化为这样的形式：

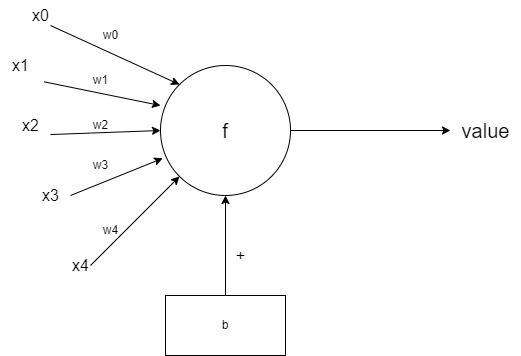
Perceptron

也就是说，左边我们可以看成一个矩阵的乘法，然后加上下面的偏置 b ，这样我们得到了一个值，假设为 temp ，然后我们通过一个函数变换 f，可能是取符号 $sign$ 函数，或其他等等，最后，我们得到了一个输出 value ，那么我们可以把这个感知机模型数学化为： $$ f(x) = \sigma(w^Tx+b) $$ 其中，我们称 $w$ 为权值矩阵，$b$ 为偏置，$\sigma$ 为激活函数。

这种图形化的形式其实我们见过很多次，被称为 神经元模型，因此，一个神经网络，就是由很多个神经元连接而成，换而言之，就是由很多个这样的感知机连接而成的，因此神经网络又被称为多层感知机（MLP）

# 网络的连接方式

在朴素的神经网络中（没有卷积没有循环什么的），我们的神经元的排列与连接是非常朴素的，我们通常将 $m_i$ 个神经元排成一排，称为网络的一层，然后我们把 $n$ 层神经元通过特定的方式连接起来，就组成了一个神经网络，如图所示：

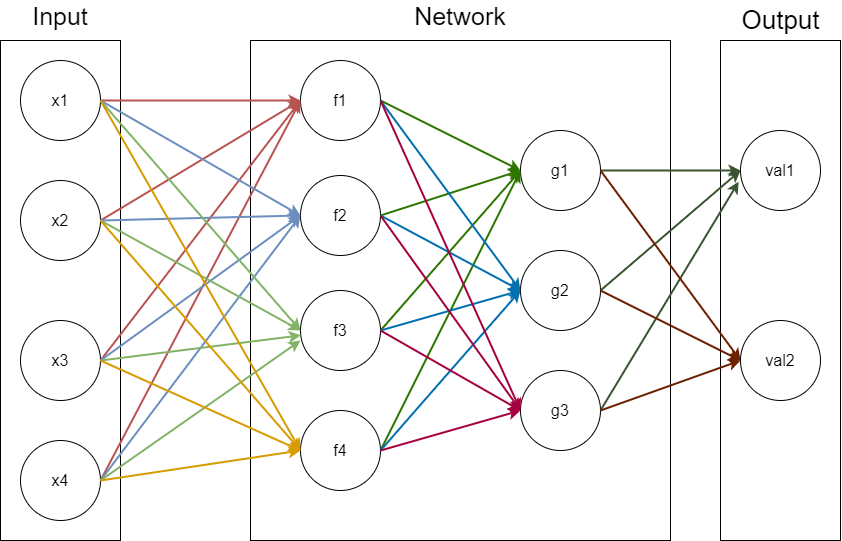
Network

我们用数学来解释一下上面这个网络。

首先，我们看到 $Input \to f_1\to g_1\to val_1$ 这个过程，注意，每一个箭头都代表了一个权值（网络中的圆代表着一个感知机），于是我们可以用这样描述：

$f_1 = \sigma(\sum^4_{i=1}w_{1i}x_i+b_{11}) = \sigma(w_{11}^Tx+b_{11})$，这里的 $w_{11}$ 是一个矩阵，代表了对应到 $f_1$ 的权值矩阵

类似的，我们可以把 $f_2, f_3, f_4$ 也用这样的形式写出来，并将其写为一个向量的话，就变成了： $$ f = (\sigma(w^T_{11}x + b_{11}), \sigma(w^T_{12}x + b_{12}), \sigma(w^T_{12}x + b_{12}), \sigma(w^T_{12}x + b_{12})) $$ 那么从 $f_1 \to g_1$ ，我们可以描述为： $$ \begin{aligned} g_1 &= \sigma(\sum^4_{i=1}f_iw_{2i} + b_{21})\ &= \sigma(w^T_{21}f+b_{21}) \end{aligned} $$ 如果我们写完整的话，就会发现这个 $g_1$ 套娃了两个 $\sigma$，而且还有一大堆 $\sum$ ，如果我们多加几层的话，最后我们表达出来的函数式会异常复杂，那么这个 $\sigma$ 到底是什么操作呢？

# 激活函数

$\sigma$ 就是我们常说的激活函数，这个函数为什么在深度学习领域很重要，就是因为只有存在这个函数，我们才能够让我们的网络符合能够拟合任意形状的函数这一特性。

我们举这样一个例子：现在你有这么多的蓝色函数，如果我给你一个红色这样的函数，你怎么用这些蓝色函数拟合出来？

Case

我们可以发现，其实我们可以通过截取这个的图形的一部分，然后加上一些截距（也就是偏置），拼凑起来得到红色的曲线：

Hard Sigmoid

但……这样似乎还不够，如果我们今天想要拟合的是曲线函数呢？比如这样的：

Case

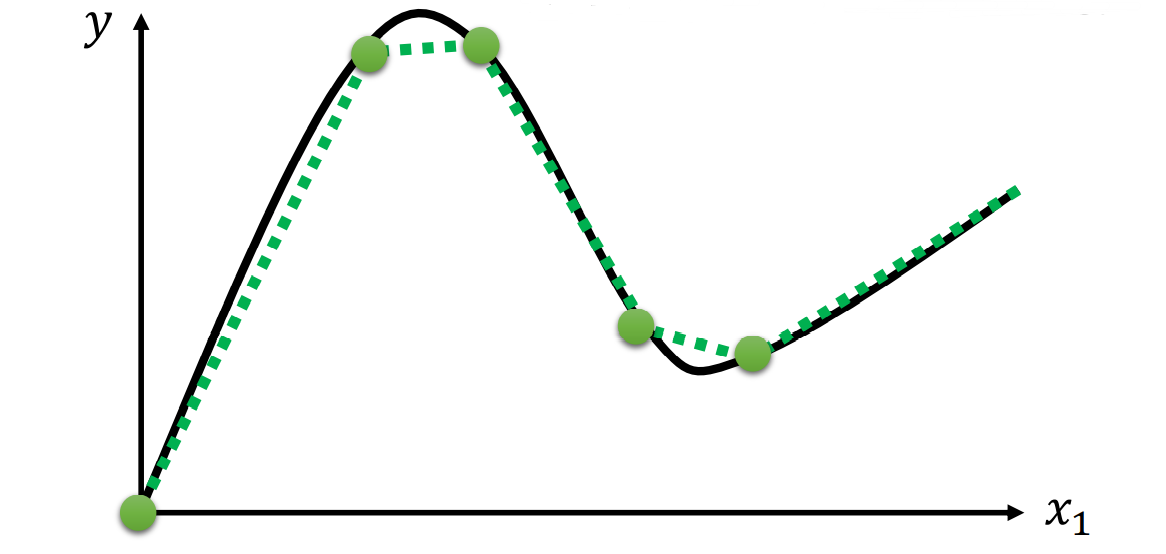
我们用刚刚那种图形就没办法很精细的拟合出来了，但别急，我们可以把我们万能的图形变得平滑一些：

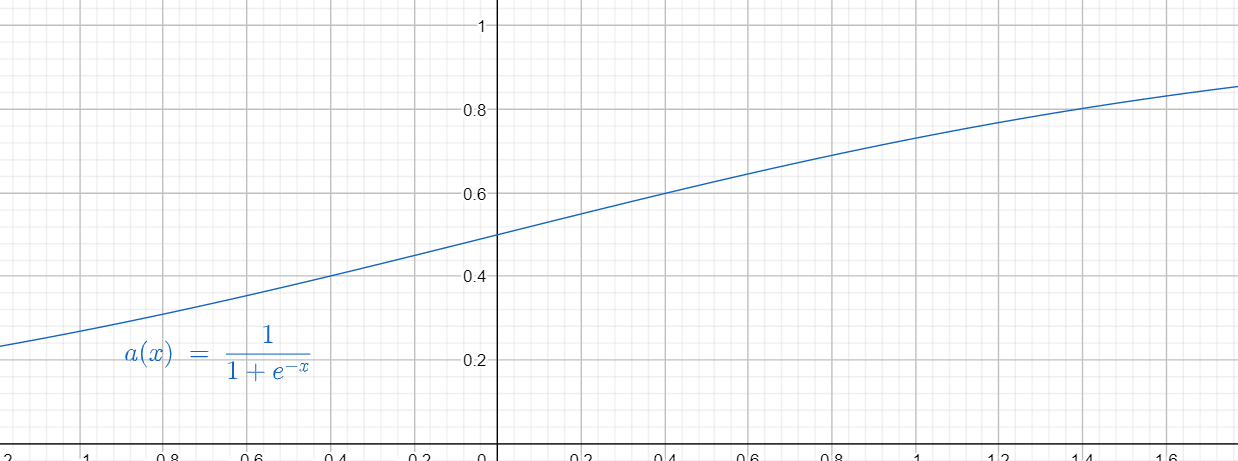
Sigmoid

我们引入这样一个函数，一个 $S$ 型的连续可导函数，并且至于在 $(0, 1)$ 之间，这样，通过线性变换（也就是截取需要的部分），我们就可以拟合任意形状的函数了。

那么，这样我们就知道激活函数到底是用来做什么的了。就是我们通过运算（权值矩阵与偏置的运算），从这个激活函数中截取出一部分来拟合原本的函数，如果精度不够，那就多加几个神经元来拟合。

用数学一些的话来解释的话就是：

如果不用激活函数，每一层输出都是上层输入的线性函数，无论神经网络有多少层，输出都是输入的线性组合，这种情况就是最原始的感知机，如果使用的话，激活函数给神经元引入了非线性因素，使得神经网络可以任意逼近任何非线性函数，这样神经网络就可以应用到众多的非线性模型中。

# 常用的激活函数

  1. sigmoid $$ \sigma(x) = \frac{1}{1+e^{-x}} $$ 值域在$(0, 1)$之间，是便于求导的平滑函数，为最常用的激活函数之一。sigmoid的导函数为： $$ \frac{d \sigma(x)}{dx} = \frac{e^{-x}}{(1+e^{-x})^2} = \sigma(x)(1-\sigma(x)) $$ 但Sigmoid有三大缺点：

    1. 容易导致梯度消失问题，是因为sigmoid函数在0和1这些区域接近饱和，梯度几乎为0，这对梯度下降来说是致命的(大多数自适应的Learning Rate是在衰减的)。
    2. sigmoid不是关于原点对称的，收敛速度慢
    3. 幂运算耗时

    虽然缺点很多，但还是经常使用，因为实在是太经典了（bushi

  2. tanh $$ tanh(x) = \frac{e^{x}-e^{-x}}{e^{x}+e^{-x}} \frac{d tanh(x)}{dx} = 1 - tanh^2(x) $$ 解决了关于原点对称的问题，但是依然存在梯度消失的问题

  3. ReLU family

    此处介绍ReLU，Leaky ReLU。ReLU 全名为 Linear rectification function

    ReLU： $$ f(x) = max(0, x) $$ 优点：

    1. 解决了梯度消失的问题
    2. 计算速度快
    3. 收敛速度快

    缺点：Dead ReLU Problem，最直观的结果就是，输入ReLU中的值如果存在负数，则最终经过ReLU之后变成0，极端情况下是输入ReLU的所有值全都是负数，则经过ReLU 之后的结果均为0。

    Leaky ReLU： $$ f(x) = max(\alpha x, x) $$ 不会有Dead ReLU问题，输出的均值接近0，它的一个小问题在于计算量稍大。

在神经网络隐藏层不多的时候，通常使用Sigmoid或tanh函数，在深度学习中常用ReLU家族的函数。

# 网络的训练（ BP 算法）

暂时不知道你们机器学习会不会学这部分，我们当时是学了的，但是统计学习方法上面没这个

放一个李宏毅的视频链接，讲的挺明白的：BP算法

2021 - 2024 © Virgil
使用 Hugo 构建