Featured image of post Two-Level Segregated Fit
我的许多零零碎碎 关于 OS 的一些零零散散

Two-Level Segregated Fit

论文的地址及其 实现 ，此文的参考解读为：TLSF解读

# 目标

论文认为一个动态内存分配器的目标主要有两个：

  • 保证 worst-case 的相应时间为 $\Theta(1)$
  • 解决内存碎片化问题

# 碎片化（Fragmentation)

碎片化（英语：fragmentation）是指存储空间使用效率低下，结果导致功能、运行效率变低或二者兼而有之的现象。碎片化所造成的影响取决于具体的存储系统以及碎片化的种类。大部分情况下，碎片化都会导致存储空间的浪费，此时“碎片”一词亦可指代闲置的空间本身。对于其他的一些系统来说（比如FAT文件系统），数据量一定的前提下，用于存储数据所占的存储空间是一定的，和碎片化的程度无关。 – 维基百科

由于我们并不将 TLSF 用于实时系统，因此在这里我们不care时间对内存分配器的严格要求

于是，内存分配器的失败的原因就变成了 内存不足。而内存不足主要有以下两个情况：

  1. 应用索求了太多的内存
  2. 内存分配算法没办法重复利用已经空闲的内存

对于第一种情况，我们能做的只有重写应用和加装内存条（显然这不是操作系统开发人员应该做的），因此我们集中解决第二种。

从历史上看，第二种情况被认为是内部和外部碎片化的两个不同方面。最近的分析认为这两个碎片分类是一个单一的问题，称为内存浪费（wasted memory）或简称碎片化（fragmentation）。

碎片化问题本质上和采取的内存分配算法有很大的关系，如果想减少内存碎片化的程度，我们有以下方法：

  1. best-fit 或 first-fit（物理内存下的）
  2. 释放时应立即合并内存块
  3. 最好重用最近释放的内存，而不是较早释放的内存块

# 算法

经典的内存分配如下所示：

  1. 顺序分配（Sequential Fit）：这些算法是最基本的算法，它们基于一个单链表或双链表来管理所有空闲内存块。基于这种策略的算法有快速分配（Fast-Fit）、首次分配（First-Fit）、循环分配（Next-Fit）和最差分配（Worst-Fit）等。但是顺序分配对于实时系统来说并不是一个好的策略，因为它基于顺序搜索，其开销取决于存在的空闲块的数量。这种搜索可能有上界，但通常不可接受。
  2. 分离空闲列表（Segregated Free Lists）：分离的空闲列表算法使用一个包含特定大小（或特定大小范围内）的空闲内存块引用的链表数组。当一个内存块被释放时，它会被插入到与其大小对应的空闲列表中。这些内存块在逻辑上是分离的，但在物理上并非如此。这种策略有两个变种：简单分离存储（Simple Segregated Storage）和分离适配（Segregated Fits）。这种策略在实时操作系统中是可接受的，因为搜索成本不依赖于空闲块的数量。
  3. 伙伴系统（Buddy Systems）：伙伴系统是分离的空闲列表的一种变种，具有高效的分割和合并操作。该方法有几个变种，如二进制伙伴、斐波那契伙伴、加权伙伴和双倍伙伴。伙伴系统表现出良好的定时行为，适用于实时操作系统；但它们的缺点是产生高达50%的大内部碎片化。
  4. 索引适配（Indexed Fit）：这种策略基于使用先进的结构来索引空闲内存块，具有几个有趣的特点。使用索引适配的算法示例包括使用平衡树的最佳适配算法，基于笛卡尔树使用两个索引（大小和内存地址）来存储空闲块的 “Fast-Fit” 分配器等。如果一个空闲块的搜索时间不依赖于空闲块的数量，索引适配策略可以比分离空闲列表表现更好。
  5. 位图适配（Bitmap Fit）：位图适配方法是索引适配方法的一种变种，它使用位图来知道哪些块是忙碌的或空闲的。这种方法的一个示例是半适配（Half-Fit）算法。相对于之前的方法，这种方法的优点是所有进行搜索所需的信息都存储在一个小的内存片段中，通常是32位，因此降低了缓存未命中的概率，并提高了响应时间。

# 操作模型

内存分配器所共有的操作为：

  1. 初始化（init)，分配器管理的内存是一个单一的、大块的空闲内存，通常称为初始池（initial pool）。也有可能分配器依赖于底层操作系统（或硬件MMU）来请求新的内存区域进行管理。
  2. 首次分配请求通过从初始池中获取内存块来满足。随后，初始池的大小会相应减小
  3. 当之前分配的内存块被释放时，根据释放块的物理位置，可能会发生两种情况：
    1. 释放的块可以与初始池或一个或多个相邻的空闲块合并；
    2. 空闲块被已分配的块所包围，无法合并。 在第一种情况下，分配算法可以合并块或将其返回给初始池。在第二种情况下，算法将空闲块插入空闲块的数据结构中。
  4. 如果存在空闲块，那么新的分配请求可以通过使用初始池或搜索足够大以适应所请求的块大小的空闲块来满足。存储空闲块的内部数据结构以及用于搜索适合的块的方法是分配器的核心，也决定了其性能。如果用于满足分配请求的空闲块比请求的大小要大，那么就需要将该块分割，并将未分配的部分返回到空闲块的数据结构中。

用户程序使用两个接口来完成内存的使用：

  • malloc
  • free

这两个接口要求内存分配器实现至少四种功能：

  1. 插入一个空闲块
  2. 搜索一个给定大小的空闲块
  3. 搜索一个块的邻居块
  4. 删除一个空闲块

# 设计

算法的设计原则为：a bounded and short response time, and a bounded and low fragmentation.

于是，设计遵循着如下标准：

  1. 立即合并：当一个内存块被释放时，分配器会立即将其与相邻的空闲内存块合并

    大多数分配算法会延迟合并，考虑到某些程序会重复使用相同内存大小的内存块，然而延迟合并会增加不可预测性和碎片。

  2. 拆分阈值：可分配的最小内存块是16字节。大多数应用，包括实时应用，很少只分配简单数据类型，而是分配复杂的数据结构。将最小块设置为16字节，可以在空闲块内存储管理信息，包括空闲块指针列表，优化内存利用。

  3. 采用 Good-fit 分配算法：TLSF会尝试返回刚好大于请求块大小的最小空闲块。由于大多数应用只用到一定范围大小的块，Good-fit 策略在实际工作负载上可以产生最少的碎片。通过分离空闲块链表可以有效实现近似 Good-fit

  4. 从不重分配：我们假设初始内存池是一个大的空闲块，没有 sbrk 接口，TLSF 完全管理动态内存

  5. 一致性：对所有需求大小都使用相同的分配策略

  6. 内存不清空：初始池和空闲块都没有被清零。在多用户环境中使用的分配算法必须清空内存（通常用零填充）以避免安全问题。

    换而言之，TLFS 只能被使用与可信环境下（也就是程序员必须完全遵守 RAII 原则）

# TLSF 数据结构

主要使用的是 隔离适配机制

  1. 使用一个数组来描述空闲列表，数组的每个单元都指向了一个固定大小的空闲块
  2. 为了加速访问空闲块并管理大量链表，并减少碎片，链表数组以两级组织：
    1. 第一级按2的幂分割块大小范围(16,32,64);
    2. 第二级线性细分每一级,细分数叫做第二级索引(SLI)

两级数据结构:第一级是指针数组，指向第二级的空闲块链表。位图标记非空链表。第二级线性划分第一级的大小范围。

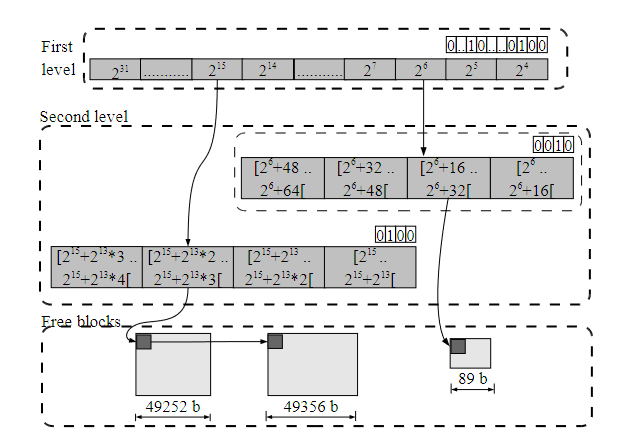
下图为一个简单的示例： image.png

第一层是指针数组，它指向空闲块的第二层列表。在这种情况下，考虑第一层的位图，只有大小范围为 $[2^6, 2^7]$ 和 $[2^{15}, 2^{16}]$ 的空闲块。第二层位图将每一个第一层范围拆分为4个隔离链表。

为了方便合并空闲块，TLSF 采用了 Knuth 提出的边界标记技术：

最初是在每个空闲或使用的块中添加一个页脚字段，该页脚字段是指向同一块开头的指针。当一个块被释放时，使用前一个块(它位于释放块之前的一个字)的脚注来访问前一个物理块的头部，以检查其是否空闲，并相应地合并两个块。通过将指针分配到块的头部，而不是在每个块的末尾，而是在下一个块的头部内部，可以简化边界标记技术。 –《CS：APP》

因此，每个空闲块被链接在两个不同的双链表中：1 )分隔链表，包含属于同一大小类的块；2 )按物理地址排序的链表。

/* The TLSF control structure. */
typedef struct control_t
{
	/* Empty lists point at this block to indicate they are free. */
	block_header_t block_null;

	/* Bitmaps for free lists. */
	unsigned int fl_bitmap;
	unsigned int sl_bitmap[FL_INDEX_COUNT];

	/* Head of free lists. */
	block_header_t* blocks[FL_INDEX_COUNT][SL_INDEX_COUNT];
} control_t;

其 Rust 实现为：

struct Tlsf {
	fl_bitmap: FLBitmap,
	sl_bitmap: [SLBitmap; FL_INDEX_COUNT],
	free_blocks: [[Option<NonNull<FreeBlockHeader>>; SL_INDEX_COUNT]; FL_INDEX_COUNT]
}

只需要记住位图为：第一层 fl_bitmap 从 $2^4$ 开始到 $2^{count}$ 结束，其中 $count$ 为自定的大小，而第二层的 sl_bitmap[i] 是固定的，其大小为 $4$

需要注意的是，$count$ 与 `FL_INDEX_COUNT` 是一样的

而关于空闲块 & 忙碌块的结构，示例图如下：

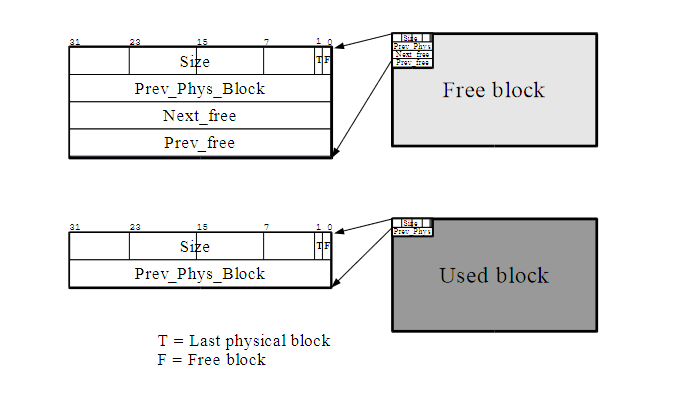
image.png

  1. 空闲块头部包含：块大小、边界标签指针、前后指针用于双向链表。
  2. 忙碌块头部只包含: 块大小和边界标签指针。
  3. 块大小总是4字节对齐，所以可以利用大小字段的两个低位来存储块状态。
  • F位表示块是否空闲
  • T位表示是否是池中的最后一个块

需要注意的是，在 Rust 实现中我们要保证结构体的内存排列与 C 中一致，并且需要保证内存的对齐（块的大小一定是 $4$ 的整数倍，这样才能保证 size 的第 $0$ 位和第 $1$ 位不会用来当作数字，而是是否使用的标识

struct BlockHeader {
	size: usize,
	prev_phys_blk: Option<NonNull<BlockHeader>>
}

struct FreeBlockHeader {
	common: BlockHeader,
	next_free: <Option<NonNull<FreeBlockHeader>>,
	prev_free: <Option<NonNull<FreeBlockHeader>>,
}

struct UsedBlockHeader {
	common: BlockHeader,
}

# 映射函数

TLSF 的大多数操作都依赖于函数 segregate list ，通过给定此函数一个需求块的大小 size ，其返回需求块第一级（first level）和第二级（second level）在 blocks 中的 index

$$ f := \lfloor\log_2(size)\rfloor $$

$$ s := (size - 2^f)\frac{2^{SLI}}{2^f} $$

对于 $f$ 的计算，本质上就是找到 size 二进制表示下从左往右第一个 $1$ 的位置

# 操作

下面列举了 tlsf 支持的操作

  • 初始化：tlsf会在内存中初始化自己的数据结构，剩余的内存被组织成为空闲池
  • 删除：将某个 tlsf 块标记为不可用
  • 搜索：返回一个恰好大于等于给定 size 的空闲块指针，这个操作分为两步：
    • 计算索引 $f$ 与 $s$，如果搜索到的链表不为空，那么会将其标记为忙状态，然后返回给用户
    • 否则，搜索下一个恰好大于等于给定 size 的链表 这种搜索可以在固定时间内使用位图掩码和查找第一组位图指令完成的
  • 插入空闲块
  • 合并空闲块：利用边界标记技术，检查前一块的头部，查看其是否为自由块。如果该块是空的，则将该块从分隔列表中移除，并与当前块合并。与下一个物理块进行相同的操作。当该块与它的自由邻块合并后，新的大块被插入到合适的隔离列表中。

# 参数

  • 第一层索引（FLI），也就是第一层的最大索引，一般计算方式为 $FLI = \min{(\log_2(memoryPoolSize), 31)}$
  • 第二层索引（SLI），细分了第一级范围。出于效率的考虑，SLI必须是2的幂次方，并且应该在 $[ 1 , 32]$ 范围内，以便使用简单的位图处理。为方便起见，将SLI表示为二级划分个数( e.g. SLI = 4，也就是将每个一级隔离类细分为16个隔离列表的对数值）

    由于不同分隔列表的数量由SLI的值决定，SLI越大，碎片化程度越小。这是一个用户自定义的参数。合理取值为4或5。

  • 最小块尺寸( Minimum Block Size，MBS )：该参数是为了限制最小块尺寸而定义的。考虑到实现的原因，MBS 常量设置为16字节。

# 一些TLSF 优化策略

  1. 缓存和 TLB 本地化策略:
  • 使用两级数组而不是二维数组，提高 cache locality
  • 将 TLSF 数据结构动态创建在内存池起始，放在同一页内提高TLB命中

2.其他策略:

  • 使用 bitmap 跟踪非空链表，限制FLI和SLI最大32，减少访问和指令数量。
  • 设计映射函数使用异或运算计算，提高效率。
2021 - 2024 © Virgil
使用 Hugo 构建