首先我们需要知道,什么是网络,什么是流。
网络
网络是指一个有向图 (不是互联网)。
每条边 都有一个权值 ,称之为容量(Capacity),当 时有 。
其中有两个特殊的点:源点(Source) 和汇点(Sink) 。
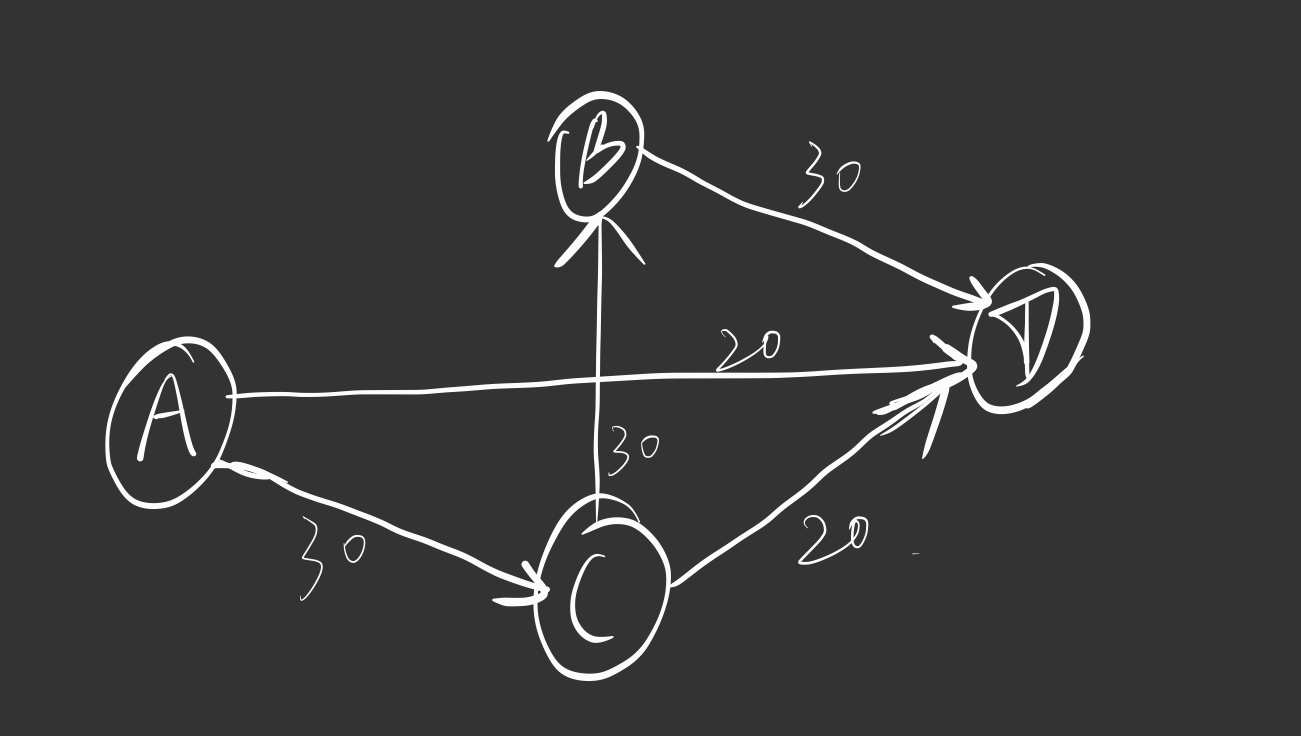
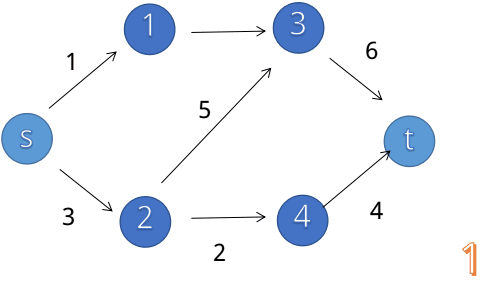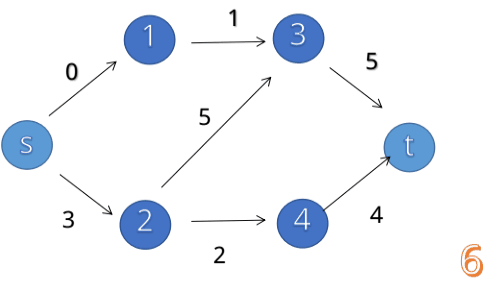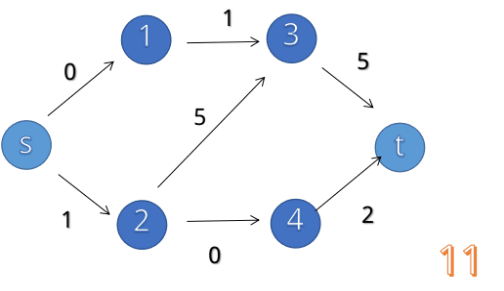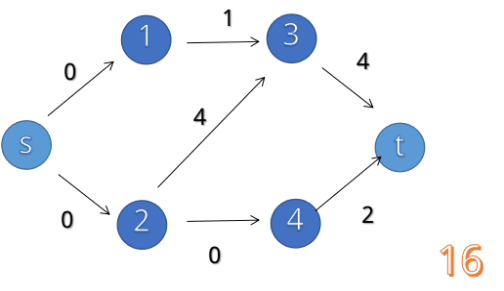
如下图所示,这就是一个网络:
其中,A为源点,D为汇点
事实上我们可以发现,源点的入度为0,汇点的出度为0
流
设 定义在二元组 上的实数函数且满足
- 容量限制:对于每条边,流经该边的流量不得超过该边的容量,即,
- 斜对称性:每条边的流量与其相反边的流量之和为 0,即
- 流守恒性:从源点流出的流量等于汇点流入的流量,即
那么 称为网络 的流函数。对于 , 称为边的 流量, 称为边的 剩余容量。整个网络的流量为 ,即 从源点发出的所有流量之和。
一般而言也可以把网络流理解为整个图的流量。而这个流量必满足上述三个性质。
注:流函数的完整定义为
网络流的常见问题
网络流问题中常见的有以下三种:最大流,最小割,费用流。
最大流问题
我们有一张图,要求从源点流向汇点的最大流量(可以有很多条路到达汇点),就是我们的最大流问题。
Ford-Fulkerson 增广路算法
该方法通过寻找增广路来更新最大流。求解最大流之前,我们先认识一些概念。
定义
- 容量: 表示一条有向边 的最大允许的流量。
- 流量: 表示一条有向边 总容量中已被占用的流量。
- 剩余容量:即 ,表示当前时刻某条有向边 总流量中未被占用的部分。
- 反向边:原图中每一条有向边在残量网络中都有对应的反向边,反向边的容量为 ,容量的变化与原边相反;反向边的概念是相对的,即一条边的反向边的反向边是它本身。
- 残量网络:在原图的基础之上,添加每条边对应的反向边,并储存每条边的当前流量。残量网络会在算法进行的过程中被修改。
- 增广路(
augmenting path):残量网络中从源点到汇点的一条路径,增广路上所有边中最小的剩余容量为增广流量。 - 增广(
augmenting):在残量网络中寻找一条增广路,并将增广路上所有边的流量加上增广流量的过程。 - 层次: 表示节点 在层次图中与源点的距离,我们以边的数量来表示。
- 层次图:在原残量网络中按照每个节点的层次来分层,只保留相邻两层的节点的图,满载(即流量等于容量)的边不存在于层次图中。
首先,我们来看看,增广路算法的过程是什么样的(一个被用烂掉的动图):
我们可以发现,这种思想遵循四个步骤:
- 找到一条从源点到汇点的路径,使得路径上任意一条边的残量 > 0
- 找到这条路径上最小的剩余容量,我们不妨设为
- 将这条路径上的每一条有向边的残量 减去 , 同时每一条有向边的反向边的残量 加上
- 重复上述过程,直到不存在增广路
那么我们会有一个问题,我们为什么要有反向边这个东西?
这是因为在做增广路时可能会阻塞后面的增广路,或者说,做增广路本来是有个顺序才能找完最大流的,但我们是任意找的,为了修正,就每次将流量加在了反向弧上,让后面的流能够进行自我调整。
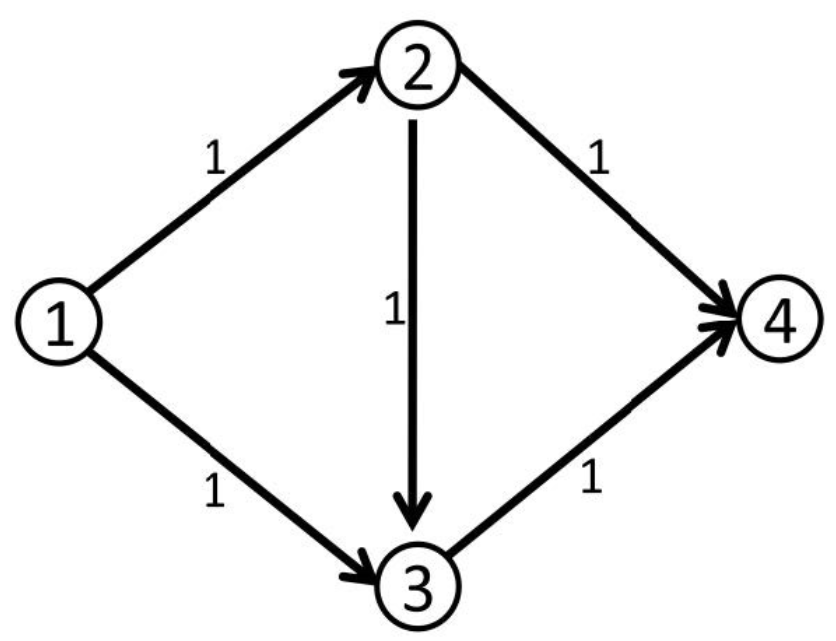
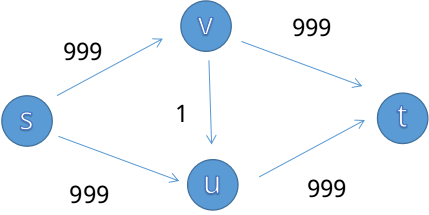
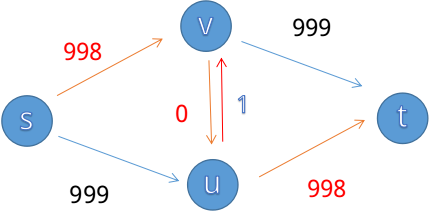
比如下面这个模型,如果我们不建立反向边的话:
我们可以找到 这条增广路,显然我们找到了一个最大流(因为没有其他增广路了)为
但实际上这个答案错误的,我们可以走 和 以得到最大流为
那么我们的算法错在什么地方呢?
问题在于,我们走 后,没有给自己留下一个后悔的机会,应该给自己一个不走 走 的机会。
所以,我们需要建立 反向边 这样一个东西,来给我们一个后悔的机会。
具体而言,我们将:
- 在找到一条增广路时,我们在路径上减去最小剩余容量的同时,还会在反向边上加上这个最小剩余容量
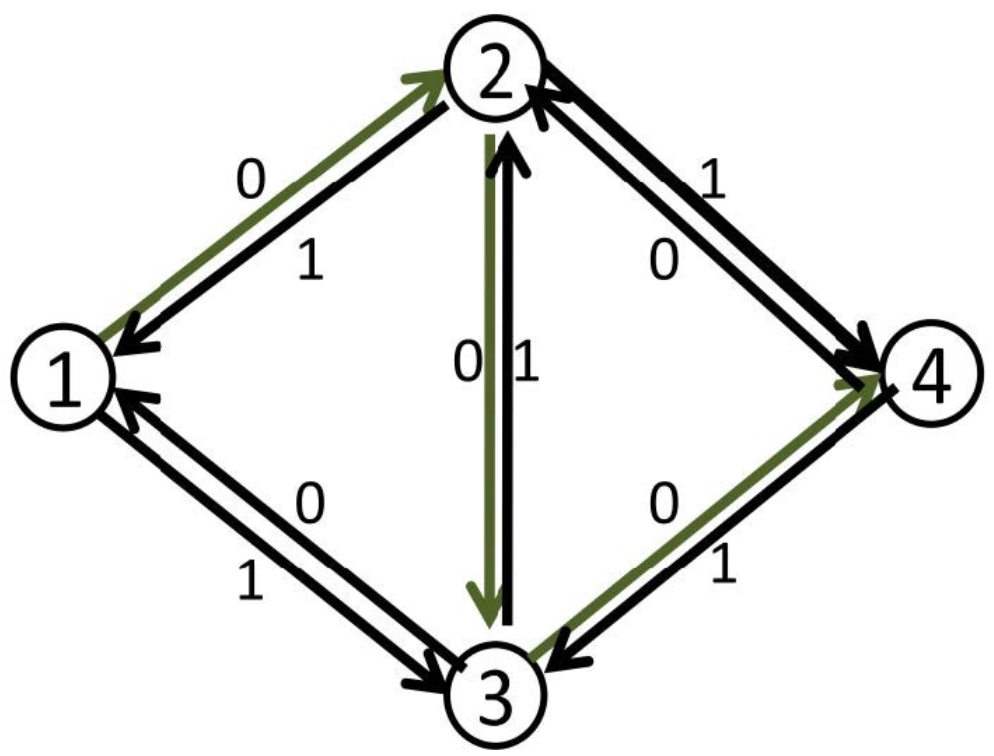
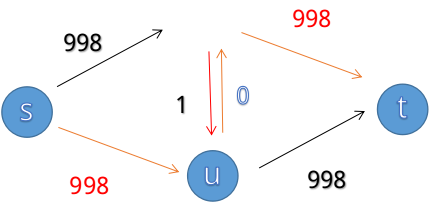
依然是上面的例子,在引入反向边后,我们找到 这条路径,我们将模型修改为:
这个时候,我们再去寻找一个增广路,我们就可以找到 这样一条增广路,这样就可以得到最大流为 。
而事实上,当我们走 这条路时,我们走过了 这一条反向边,也就相当于说,我们把原来 这条边的流量给退回去了,不 走 这条路,相当于是为第一次的天真选择买了一次后悔药(bushi
Bug
Dinic 算法
Dinic 算法 的过程是这样的:每次增广前,我们先用 BFS 来将图分层。设源点的层数为 ,那么一个点的层数便是它离源点的最近距离。
通过分层,我们可以干两件事情:
- 如果不存在到汇点的增广路(即汇点的层数不存在),我们即可停止增广。
- 确保我们找到的增广路是最短的。
接下来是 DFS 找增广路的过程。
我们每次找增广路的时候,都只找比当前点层数多 的点进行增广(这样就可以确保我们找到的增广路是最短的)。
举一个例子来解释:
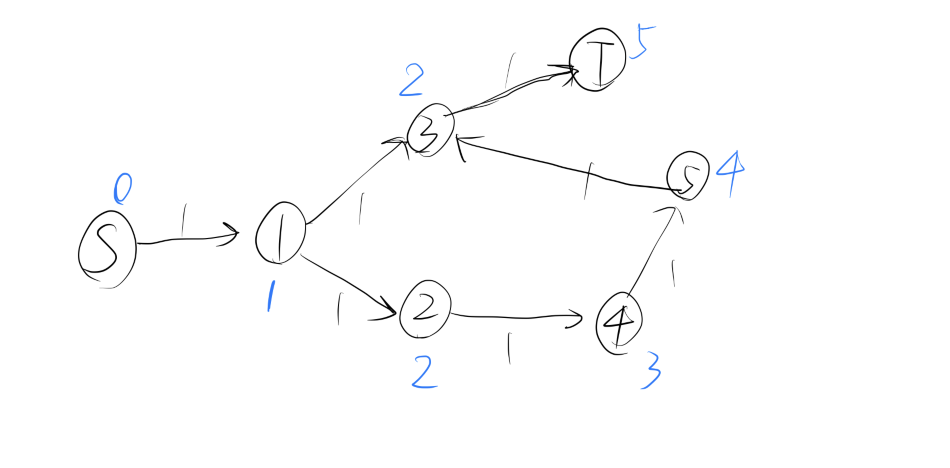
如果有分层的话(蓝色表示每个节点的层数),我们就一定不会选择 ,因为 的层数比 要小,不可能在 后才被拓展。
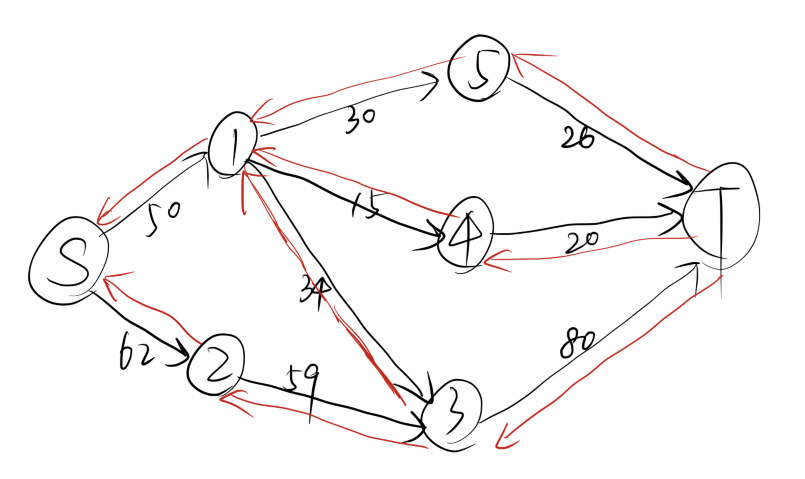
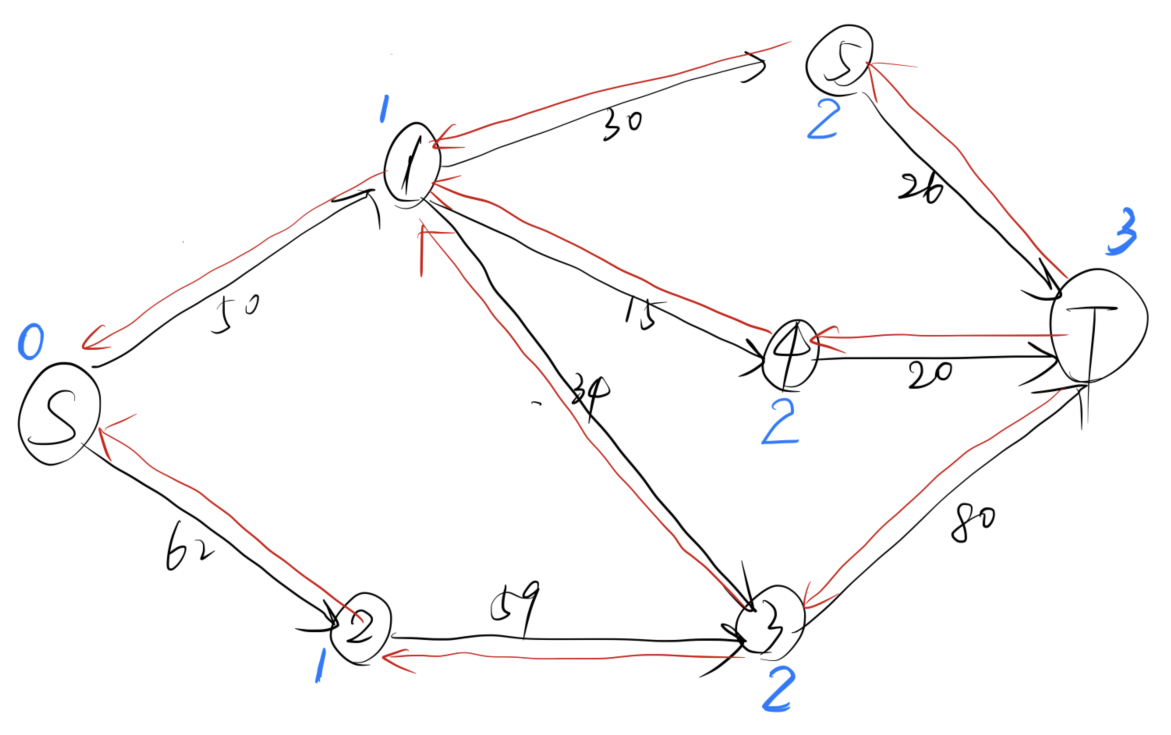
我们使用这个案例来解释 Dinic 都做了什么:
随后,我们会对这个网络进行分层:
我们发现,汇点的层数存在,因此存在增广路,于是我们通过 dfs 来寻找:
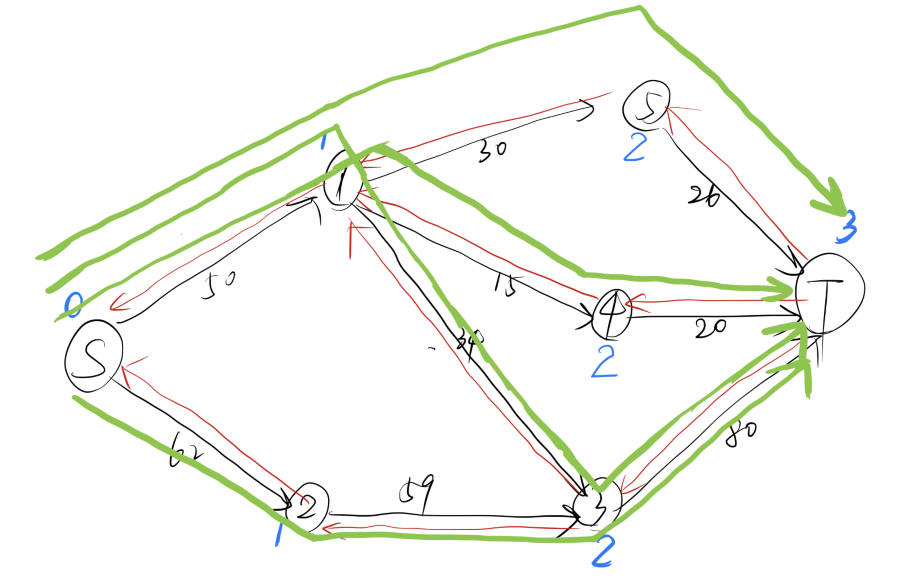
我们从 出发,首先找到 ,回溯后找到 ,再次回溯后找到 ,最后,我们还能找到
这样,一次 dfs 我们就能找到4条增广路(高效的算法)
随后,我们会重复使用 BFS 对残量网络进行分层,并使用 DFS 进行增广路寻找,直到汇点层数为零,我们就求出了最大流。
代码如下:
#define maxn 250#define INF 0x3f3f3f3f
struct Edge { int from, to, cap, flow;
Edge(int u, int v, int c, int f) : from(u), to(v), cap(c), flow(f) {}};
struct Dinic { int n, m, s, t; vector<Edge> edges; vector<int> G[maxn]; int d[maxn], cur[maxn]; bool vis[maxn];
void init(int n) { for (int i = 0; i < n; i++) G[i].clear(); edges.clear(); }
void AddEdge(int from, int to, int cap) { edges.push_back(Edge(from, to, cap, 0)); edges.push_back(Edge(to, from, 0, 0)); m = edges.size(); G[from].push_back(m - 2); G[to].push_back(m - 1); }
bool BFS() { memset(vis, 0, sizeof(vis)); queue<int> Q; Q.push(s); d[s] = 0; vis[s] = 1; while (!Q.empty()) { int x = Q.front(); Q.pop(); for (int i = 0; i < G[x].size(); i++) { Edge& e = edges[G[x][i]]; if (!vis[e.to] && e.cap > e.flow) { vis[e.to] = 1; d[e.to] = d[x] + 1; Q.push(e.to); } } } return vis[t]; }
int DFS(int x, int a) { if (x == t || a == 0) return a; int flow = 0, f; for (int& i = cur[x]; i < G[x].size(); i++) { Edge& e = edges[G[x][i]]; if (d[x] + 1 == d[e.to] && (f = DFS(e.to, min(a, e.cap - e.flow))) > 0) { e.flow += f; edges[G[x][i] ^ 1].flow -= f; flow += f; a -= f; if (a == 0) break; } } return flow; }
int Maxflow(int s, int t) { this->s = s; this->t = t; int flow = 0; while (BFS()) { memset(cur, 0, sizeof(cur)); flow += DFS(s, INF); } return flow; }};Dinic 算法有两个优化:
- 多路增广:每次找到一条增广路的时候,如果残余流量没有用完怎么办呢?我们可以利用残余部分流量,再找出一条增广路。这样就可以在一次 DFS 中找出多条增广路,大大提高了算法的效率。
- 当前弧优化:如果一条边已经被增广过,那么它就没有可能被增广第二次。那么,我们下一次进行增广的时候,就可以不必再走那些已经被增广过的边。
时间复杂度
设点数为 ,边数为 ,那么 Dinic 算法的时间复杂度(在应用上面两个优化的前提下)是
首先考虑单轮增广的过程。在应用了 当前弧优化 的前提下,对于每个点,我们维护下一条可以增广的边,而当前弧最多变化 次,从而单轮增广的最坏时间复杂度为 。
接下来我们证明,最多只需 轮增广即可得到最大流。
我们先回顾下 Dinic 的增广过程。对于每个点,Dinic 只会找比该点层数多 的点进行增广。
首先容易发现,对于图上的每个点,一轮增广后其层数一定不会减小。而对于汇点 ,情况会特殊一些,其层数在一轮增广后一定增大。
对于后者,我们考虑用反证法证明。如果 的层数在一轮增广后不变,则意味着在上一次增广中,仍然存在着一条从 到 的增广路,且该增广路上相邻两点间的层数差为 。这条增广路应该在上一次增广过程中就被增广了,这就出现了矛盾。
从而我们证明了汇点的层数在一轮增广后一定增大,即增广过程最多进行 次。
综上 Dinic 的最坏时间复杂度为 。事实上在一般的网络上,Dinic 算法往往达不到这个上界。
特别地,在求解二分图最大匹配问题时,Dinic 算法的时间复杂度是 。接下来我们将给出证明。
首先我们来简单归纳下求解二分图最大匹配问题时,建立的网络的特点。我们发现这个网络中,所有边的流量均为 ,且除了源点和汇点外的所有点,都满足入边最多只有一条,或出边最多只有一条。我们称这样的网络为 单位网络。
对于单位网络,一轮增广的时间复杂度为 ,因为每条边只会被考虑最多一次。
接下来我们试着求出增广轮数的上界。假设我们已经先完成了前 轮增广,因为汇点的层数在每次增广后均严格增加,因此所有长度不超过 的增广路都已经在之前的增广过程中被增广。设前 轮增广后,网络的流量为 ,而整个网络的最大流为 ,设两者间的差值 。
因为网络上所有边的流量均为 ,所以我们还需要找到 条增广路才能找到网络最大流。又因为单位网络的特点,这些增广路不会在源点和汇点以外的点相交。因此这些增广路至少经过了 个点(每条增广路的长度至少为 ),且不能超过 个点。因此残量网络上最多还存在 条增广路。也即最多还需增广 轮。
综上,对于包含二分图最大匹配在内的单位网络,Dinic 算法可以在 的时间内求出其最大流。
题外(一种更好写也更快的算法)
在 Dinic 算法中,我们每次求完增广路后都要跑 BFS 来分层,有没有更高效的方法呢?
答案就是 ISAP 算法。
大家可以自己去学一学 ISAP 算法(