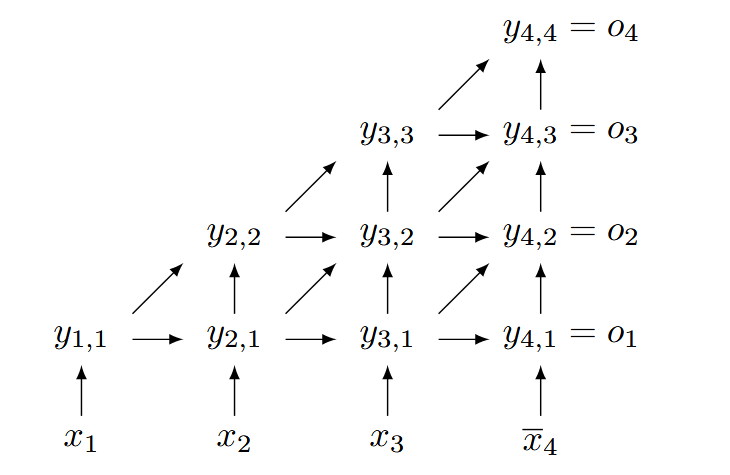基数约束编码中文字顺序的重要性

Tldr

文章链接

The Impact of Literal Sorting on Cardinality Constraint Encodings

Summary

The effectiveness of satisfiability solvers strongly depends on the quality of the encoding of a given problem into conjunctive normal form. Cardinality constraints are prevalent in numerous problems, prompting the development and study of various types of encoding. We present a novel approach to optimizing cardinality constraint encodings by exploring the impact of literal orderings within the constraints. By strategically placing related literals nearby each other, the encoding generates auxiliary variables in a hierarchical structure, enabling the solver to reason more abstractly about groups of related literals. Unlike conventional metrics such as formula size or propagation strength, our method leverages structural properties of the formula to redefine the roles of auxiliary variables to enhance the solver’s learning capabilities. The experimental evaluation on benchmarks from the maximum satisfiability competition demonstrates that literal orderings can be more influential than the choice of the encoding type. Our literal ordering technique improves solver performance across various encoding techniques, underscoring the robustness of our approach.

基数约束

考虑变量集合 $X=\{x_1,x_2\dots ,x_n\}$，我们有如下约束：

$$x_1+x_2+\cdots +x_n\#K$$

其中，$K\in \mathbb{N},x_i\in \{0,1\},\#\in \{\le ,\ge =\}$

我们将此类约束称之为基数约束，值得注意的是，基数约束中的 $\ge ,\le$ 可以通过 $x_i+\neg x_i=1$ 相互转化，而 $=$ 可以通过 $\ge ,\le$ 来进行夹逼。

编码方式

这里我们介绍当前三种常用的编码方式，假设我们当前编码的约束为:

$$x_1+x_2+x_3+\neg x_4\le 2$$

Sequential Counter

我们的编码方式如下图所示，我们称 $x_i,\neg x_i$ 为数据文字：

这里若 $y_{i,j}$ 为真，当且仅当前 $i$ 个数据文字至少有 $j$ 个为真

那么最后一列中的 $y_{n,j}$ 就表示该基数约束中至少有 $j$ 个文字为真（至多有 $n-j$ 个文字为假）

换而言之，如存在基数约束：$x_1+\cdots +x_n\ge K$，那么我们只需要保证 $y_{n,K}$ 为真即可（单元子句）。

而当约束为 $\le$ 时，那么必然不能有  $K+1$  个或更多文字为真，于是我们可以轻易的得到单元子句 $\neg y_{n,K+1}$，也就是图中的 $\neg o_3$

于是对于我们示例，本质上我们只需要下面三行，不需要编码到 $o_4$，我们通过动态规划的方式进行编码：

$$\begin{array}{rl}{y}_{i+1,j}& \leftarrow y_{i,j}\\ y_{i,j+1}& \leftarrow (y_{i-1,j}\wedge x_i)\end{array}$$

我们可以发现这种编码方式是非对称的，辅助变量 $y_{i,j}$ 从左到右承载的信息从少到多，例如上图中，我们可以通过 $y_{2,1},y_{2,2}$ 中的任意一个推理出 $x_1,x_2$ 的值（ $y_{1,2}$ 知道两个中至少一个为真，$y_{2,2}$ 知道两个都为真），然而，我们找不到任何一个辅助变量能够帮助我们只推理 $x_3,\neg x_4$ 的赋值。

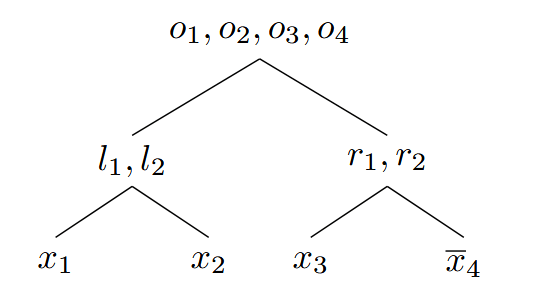
Tree-Based

第二个方法我们通过一棵二叉树来实现：

此二叉树在每一层都会计算为真的数据文字数，并依次增加。数据文字组成了二叉树的叶子，其他的节点为辅助变量，辅助变量的下标为其子节点下标的序数之和，例如这里，若 $o_3$ 为真，那么表示 $l_1,r_2$ 或 $l_2,r_1$ 有一对均为真。

和前面的编码类似，当约束为 $\le$ 时，那么必然不能有  $K+1$  个或更多文字为真，那么只需要添加单元子句 $\neg o_{K+1}$ 即可

Note

当然，这种编码方式还有其他优化，用于减少辅助变量的数目

我们可以发现，这种编码方式是对称的，因为我们可以通过辅助变量 $r_1,r_2$ 来推理出 $x_3,\neg x_4$ 的赋值情况

然而，如果文字在叶子节点相距的越远，我们就需要更深的树才能够将其结合在一起，例如 $x_1,\neg x_4$ 只有在根节点时，才会共享一个抽象结构。可以发现这种编码方式也是排序敏感的，如果我们有着正确的次序，那么可能通过一次推理就能够获得更多的信息。

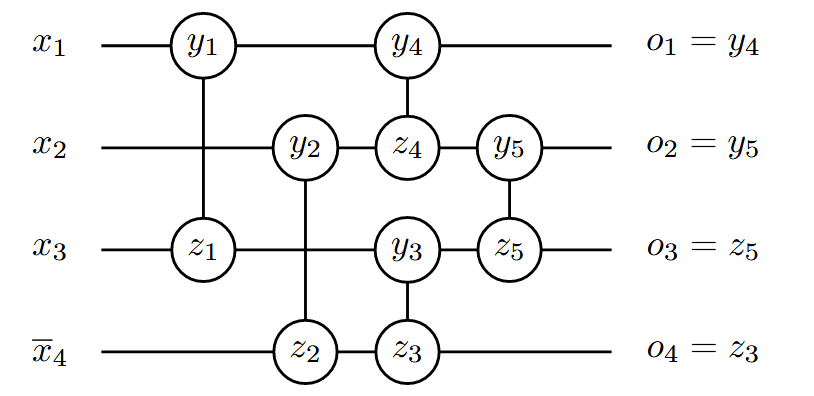
Cardinality Networks

网络的编码方式可以查看 Conflict Directed Lazy Decomposition 中的编码示例，在这里我们不再详细介绍其过程：

可以发现，这种网络结构虽然是对称的，但其本质上也是排序敏感的，因为每次其通过门时，都是按照两两分组来实现的，那么分组的顺序或许就会显得十分重要。对上图中的数据文字进行 shuffle 并不会改变最终子句和变量的多少，但会改变辅助变量的含义。

Literal Sorting Methods

在这一部分，我们提供了几种排序方法来辅助上文中的编码，根据时间复杂度的从小到大，这些方法为：Natural, Random, Occur, Proximity, PAMO, Graph

我们考虑的例子为：

$$\begin{array}{rl}& (x_1\vee x_2)\wedge (\neg x_1\vee x_2)\wedge (\neg x_2\vee x_3\vee x_4)\wedge (\neg x_4\vee x_5)\\ & x_1+x_2+x_3+\neg x_4\le 2\end{array}$$

Natural 的方法最为简单，通过给定变量的编号直接进行排序，那么我们得到的基数约束为 $x_1+x_2+x_3+\neg x_4\le 2$

Random 的方法通过一个随机排列来对变量进行排序，纯粹的碰运气方法

Occur 通过统计变量在子句中出现的次数（正负文字都统计），根据出现次数的递减顺序进行排序（因为 Sequential Counter 为这种不平衡提供了最多的推理能力，保证稠密的变量出现在前面，稀疏的在后面），那么我们得到的基数约束为 $x_2+x_1+\neg x_4+x_3\le 2$

Proximity 与 PAMO 通过 基数约束SAT的精确求解器 中提到的基数探测，从子句中探测出那些变量数大于等于 5 个的基数约束，我们将这些约束简称为 AMO。其工作流程可以视为一个 BFS，如下所述：

1. 选择一个未被选择过的具有最高分数的变量 $v$，如果当前最高分数为 $0$，那么我们选择那个在子句中出现次数最多的未被选择过的变量 $v$
2. 我们将变量 $v$ 追加到排序后列表的末尾
3. 如果基数探测被激活了，那么对于每一条 AMO 约束，如果这条约束含有变量 $v$ 的任意文字，那么我们将这条约束中其余的未被选择过的变量的分数增加 $le{n}^2$ ，$len$ 为约束的长度
4. 而对于每一条含有变量 $v$ 的子句，我们将子句中其余的未被选择过的变量的分数增加 $\frac{1}{|C|}$ (如果子句长度大于等于 3，否则直接增加 4)
5. 如果所有出现在基数约束（非 AMO）中的变量都被处理了，那么我们也得到了一个排序。

可以发现，即使不使用基数探测 AMO，Proximity 的时间复杂度也可以达到 $O(n^3)$ 。那么单独的 Proximity 得到的基数约束为：$x_2+x_1+x_3+\neg x_4\le 2$

Graph 通过变量为节点，是否在一条子句内为边构成的一张无向图，这里我们使用的社区检测的方法，找到那些合适的社区，我们会运行多次，找到不同的解，例如：

$$\begin{array}{rl}{S}_1& =\{C_{1,1}=\{x_1,x_3,x_5\},C_{1,2}=\{x_2,x_4\}\}\\ S_2& =\{C_{2,1}=\{x_1,x_3,x_5\},C_{2,2}=\{x_2\},C_{2,3}=\{x_4\}\}\\ S_3& =\{C_{3,1}=\{x_1,x_3\},C_{3,2}=\{x_2,x_5\},C_{3,3}=\{x_4\}\}\end{array}$$

然后，我们每次选择那些具有更多数量的社区，这里我们选择 $S_2,S_3$ ，然后我们选择社区平均大小最小的解，这里我们选择 $S_3$ ，最后，我们将那些出现在基数约束中的变量按照社区里出现的顺序进行拼接：$x_1+x_3+x_2+\neg x_4\le 2$

实验

MaxSAT 很适合作为基数约束编码/求解的 benchmark，原因可以看Conflict Directed Lazy Decomposition

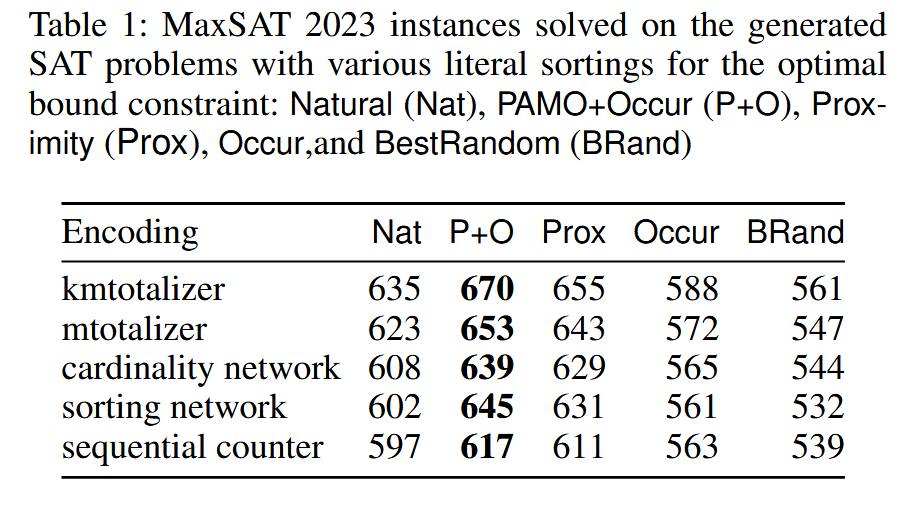
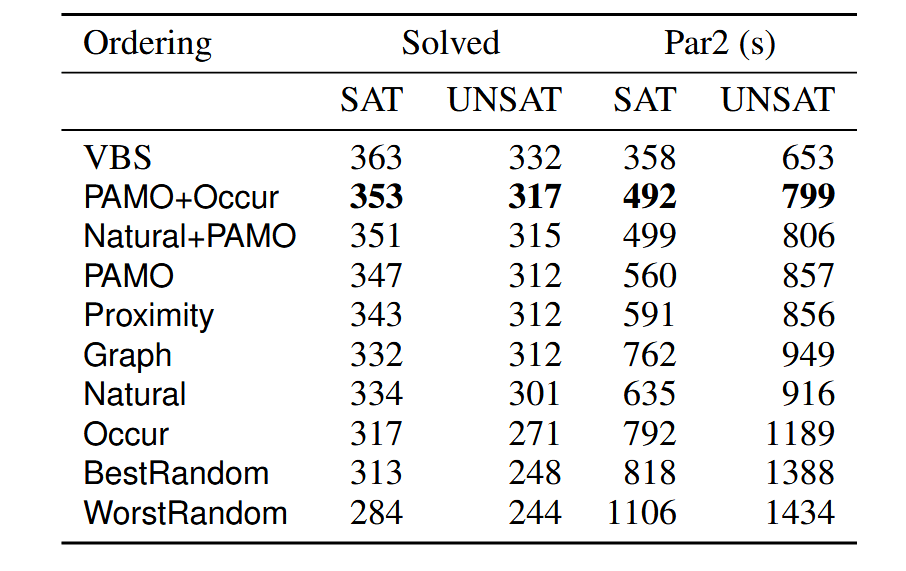
表中的 PAMO + Occur 意思是对少于 100 万个子句的公式运行 PAMO，否则使用 Occur 排序

接着，我们后面均使用基于 Tree-Based 优化的编码 kmtotalizer 来进行编码，然后进行 SAT 求解：

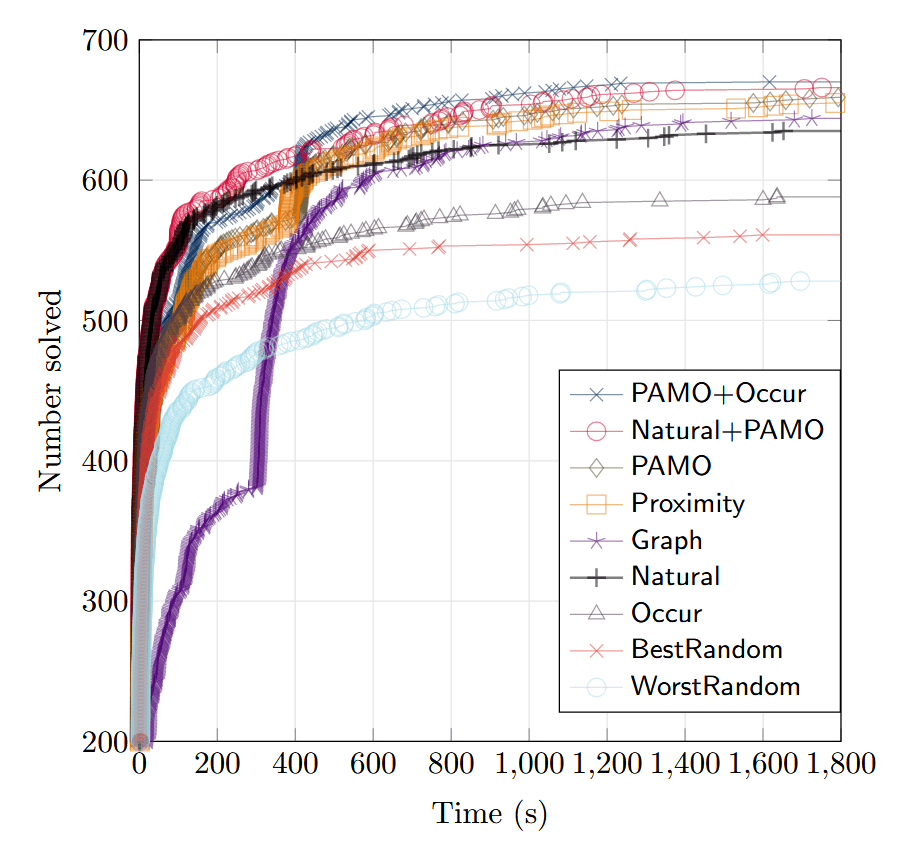
其中 VBS 是理论最优求解器的结果，可以视为 baseline，求解时间与求解个数的图如下所示：