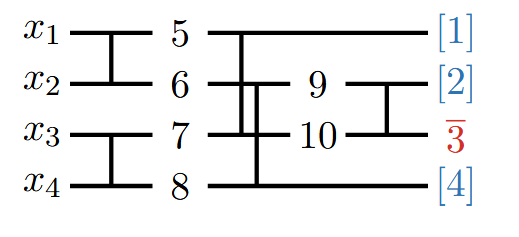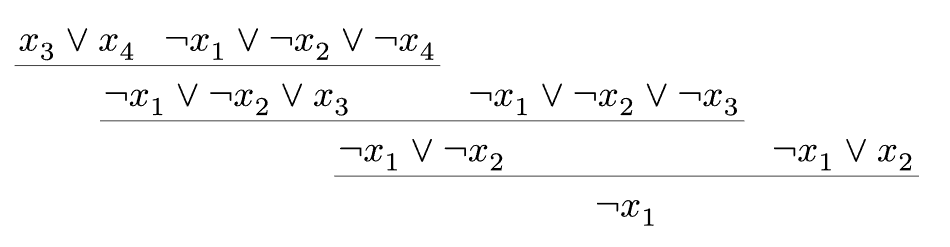Tldr

文章链接

在 SAT 问题的全局约束中，如果将约束编码为 SAT，会导致变量与子句的急速膨胀，造成求解困难。但有时候，编码的辅助变量又属于 nogood 类型的变量，能够指导搜索的过程。

因此本文提出了一种求解器框架，在约束传播的过程中，我们有选择的分解（编码）那些 nogood 类型的变量，使得能够更快的求解问题。

查看 Slides

Conflict Directed Lazy Decomposition

Summary

Two competing approaches to handling complex constraints in satisfaction and optimization problems using SAT and LCG/SMT technology are: decompose the complex constraint into a set of clauses; or (theory) propagate the complex constraint using a standalone algorithm and explain the propagation. Each approach has its benefits. The decomposition approach is prone to an explosion in size to represent the problem, while the propagation approach may require exponentially more search since it does not have access to intermediate literals for explanation. In this paper we show how we can obtain the best of both worlds by lazily decomposing a complex constraint propagator using conflicts to direct it. If intermediate literals are not helpful for conflicts then it will act like the propagation approach, but if they are helpful it will act like the decomposition approach. Experimental results show that it is never much worse than the better of the decomposition and propagation approaches, and sometimes better than both.

Global Constraints

我们首先介绍两种约束类型：

1. 基数约束 考虑变量集合 $X=\{x_1,x_2\dots ,x_n\}$，我们有如下约束：

   $$x_1+x_2+\cdots +x_n\#K$$

   其中，$K\in \mathbb{R},x_i\in \{0,1\},\#\in \{\le ,\ge =\}$

2. 伪布尔约束 考虑变量集合 $X=\{x_1,x_2\dots ,x_n\}$，我们有如下约束：

   $$a_1{x}_1+\cdots +a_n{x}_n\#K$$

   其中，$a_i,K\in \mathbb{R},x_i\in \{0,1\},\#\in \{\le ,\ge =\}$

这两种约束，其约束的集合均为变量集合，因此被称为全局约束

对于这两类常见的全局约束，我们常用的有两种方法：

1. decomposition(或称为 encoding)：编码为 SAT，使用 SAT 求解器进行求解
2. Lazy Clause Generation：使用 SMT 方法进行求解，这里我们简称为约束传播

我们以基数约束为例，解释这两种方法

Decomposition

我们考虑一个常用的编码 Cardinality Network， 其通过多个 2-comparators 来构建的，一个比较算子的电路结构为 $2-comp(x_1,x_2,y_1,y_2)$，其中，$x_1,x_2$ 为输入，$y_1,y_2$ 为输出，满足以下约束：

$$y_1=x_1\vee x_2,y_2=x_1\wedge x_2$$

这个电路能够很轻松的编码为 SAT，对于 $\ge$ 约束而言：

$$\begin{array}{rl}\neg x_1& \vee y_1\\ \neg x_2& \vee y_1\\ \neg x_1\vee & \neg x_2\vee y_2\end{array}$$

对于 $\le$ 约束而言：

$$\begin{array}{rl}\neg x_1& \vee \neg y_2\\ \neg x_2& \vee \neg y_2\\ x_1\vee & x_2\vee \neg y_1\end{array}$$

Cardinality Network 是一个通过 $k$ 个比较算子连接起来的电路结构，有 $n$ 个输入和输出，且需要满足以下两个性质：

1. 为真的输出个数与为真的输入个数相同
2. 对任意 $1\le i\le k$ ，当且仅当电路的输入至少有 $i$ 个为真时，第 $i$ 个输出才为真

编码示例

考虑以下例子：

$$x_1+\cdots +x_4\ge 3$$

我们构造一个 $k+1$ 的Cardinality Network如下：

这个电路可以很轻易的表述为 SAT 子句的形式，最后，根据基数约束，由于输入至少三个为真，于是输出也至少有三个为真，于是第 $3$ 个输出是真

我们只需要最后加上一条单元子句，使得第三个输出为真即可

Lazy Clause Generation

我们首先介绍什么是 Lazy Clause Generation

Tldr

对于一个由公式 $F$ 与一个约束集合 $\{c_i\}$ 构成的约束满足问题，LCG 由两部分组成：SAT 求解器和每个约束 $c_i$ 的传播函数。 SAT 求解器判定公式是否可满足并给出满足赋值，传播函数推导赋值的结果和约束集（即约束传播），并为 SAT 求解器提供一些传播文字的原因（称为解释）。

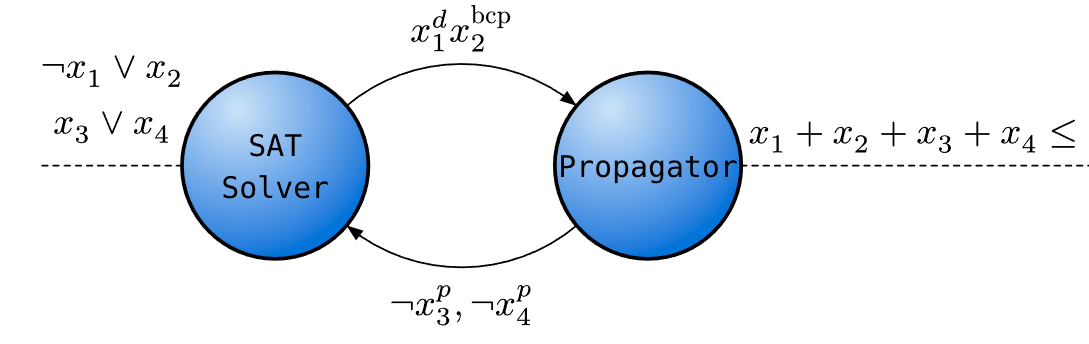
考虑以下例子：$\neg x_1\vee x_2,x_3\vee x_4,x_1+x_2+x_3+x_4\le 2$，求解的框架如下：

发现冲突，传播函数给出原因如下：

$$\begin{array}{rl}\neg x_3& =\neg x_1\vee \neg x_2\vee \neg x_3\\ \neg x_4& =\neg x_1\vee \neg x_2\vee \neg x_4\end{array}$$

接着，我们给出归结如下：

于是 SAT 求解器得到学习子句 $\neg x_1$

Lazy Decomposition

分解与 LCG 各有其优势，考虑以下两种情况：，考虑以下两种情况：

• 考虑一个由上百条基数约束构成的问题，如果我们将其分解为 SAT，会引入巨量的辅助变量与子句，使得求解效率急速降低，这个时候如果使用约束传播方法就会快很多

• 考虑一个基数约束 ${\sum }_i{x}_i\le K$ 的问题，但这个问题中的一些子句可以推导（归结）出以下约束 ${\sum }_i{x}_i\ge K+1$ ，使得问题直接变成 UNSAT，这个时候对于约束传播算法，我们无法快速找到矛盾，可能需要枚举所有可能的结果来证明问题是 UNSAT 的，但如果我们分解为 SAT 问题，我们甚至可以在预处理阶段就发现这个矛盾

我们的基本假设是：对于每个问题，将其分解为 SAT 时都会产生一些有助于 SAT 求解的辅助变量以及另一部分加大求解难度的无用辅助变量

于是，我们期望如何在分解时只生成那些对 SAT 求解有帮助的辅助变量

LD 框架

Lazy Decomposition 的做法与 LCG 的很相似，本质上是一个 LCG 与编码的结合求解方法，与 LCG 不同的是，LCG 的传播函数只做传播和推导（或者说解释），但 Lazy Decomposition 中的传播函数除了传播外，还需要探测编码哪些变量为 SAT 对求解是有帮助的。

一个 Lazy Decomposition 求解器必须要做到以下几点：

1. （动态地）识别编码哪些变量有助于学习子句的生成
2. 无论约束有没有被编码（或者被部分编码），算子都必须能够正确进行约束传播
3. 避免传播当前编码的约束

我们以基数约束中的懒编码为例，详细解释这个求解器是如何工作的。

基数约束中的 LD

考虑如下基数约束：

$$x_1+x_2+x_3+x_4+\cdots +x_n\le K$$

Hint

$\ge ,=$ 都可以转化为 $\le$ 类型的约束

根据 编码过程 中所知的，对于 2-comp 门，由于 $y_1=x_1\vee x_2,y_2=x_1\wedge x_2$，于是有如下性质成立：

$$x_1+x_2=y_1+y_2$$

那么，我们可以将原基数约束改写为：

$$y_1+y_2+x_3+\cdots +x_n\le K$$

然后将其再次编码为 SAT 语句，相当于我们为 SAT 求解器引入了两个新变量 $y_1,y_2$，当这样的替换发生后，传播函数通过用新定义的变量替换旧变量来传播基数约束

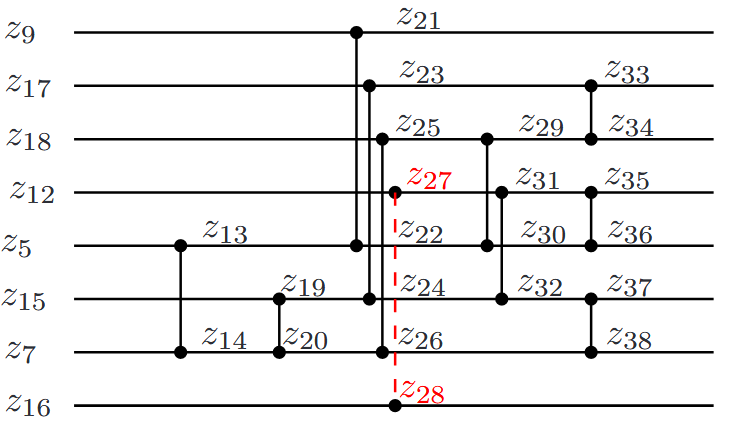
Example

考虑一个 8 个变量的基数约束 $x_1+\dots x_8\le 3$，其电路图如下所示（如果完全编码为 SAT）：

这时，如果我们只编码前两层的话，也就是只引入新变量 $z_1,\dots ,z_{12}$，就可以将基数约束写为

$$z_5+z_6+\cdots +z_{12}\le 3$$

传播函数必须确定应该添加到 SAT 求解器中的分解部分。为了提高效率，求解器仅在执行重启时才添加变量：重启发生得足够频繁，以确保生成重要变量不会太晚，但又不会过于频繁，以免显著影响求解器性能。此外，在搜索的根节点添加变量和子句要容易得多。

Cite

在约束满足问题（CSP, Constraint Satisfaction Problem）中，nogood  是指一组变量的赋值组合，这些组合违反了问题中的一个或多个约束条件

当求解器发现一个冲突（即当前的变量赋值违反了约束），它会回溯并生成一个 nogood，表示导致冲突的赋值组合。

如何分解

传播函数为每个约束中的变量 $x_i$ 都维护了一个数值 $ac{t}_i$，每当有一次 nogood 被生成时，包含在 nogood 中的所有变量的 $ac{t}_i$ 都会自增 $1$

每当求解器重启时，传播函数都会检查在约束中，是否存在 $ac{t}_i\ge \lambda N$ ，其中 $\lambda$ 是设定的参数，$N$ 表示上一次重启后发生的所有冲突数。如果 $ac{t}_i\le \lambda N$，那么 $ac{t}_i=\frac{ac{t}_i}{2}$ （带有遗忘机制），否则我们考虑以下三种情况：

1. 如果 $x_i$ 不是 2-comp 门的输入，什么都不做
2. 否则， $x_i$ 是 2-comp 门的输入，我们考虑两种情况：
   1. 这个门的另一个输入 $x_j$ 已经被前面的变量编码生成了，那么我们直接使用$y_i+y_j$ 替换 $x_i+x_j$，并编码为 SAT 子句
   2. 这个门的另一个输入 $x_j$ 还没有被生成，我们做如下处理： 考虑集合 $S=\{x_{k_1},x_{k_2},\dots ,x_{k_s}\}$，其表示当前约束中的一些变量，经过若干分解与编码步骤后，这些变量可以导出 $x_j$。那么，我们对所有输入都出现在  $S$  中的 2-comp 执行分解步骤，以得到 $x_j$，接着，我们使用 $y_i+y_j$ 替换 $x_i+x_j$ 并编码为 SAT 子句

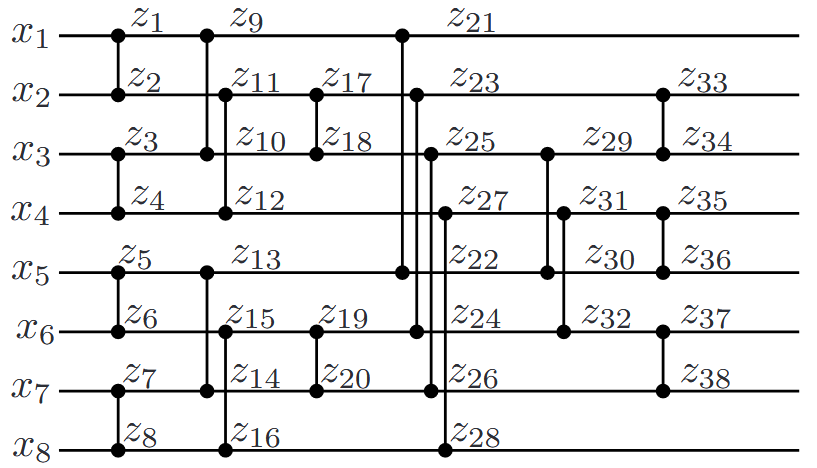
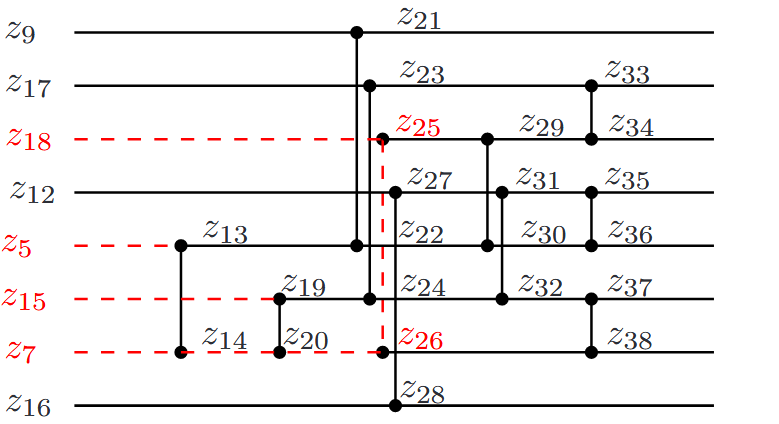
Example

考虑基数约束 $x_1+\cdots +x_8\le 3$，在经过一些求解步骤后，现在的约束变为：$z_9+z_{17}+z_{18}+z_{12}+z_5+z_{15}+z_7+z_{16}\le 3$，具体电路图如下：

当前未被生成的电路门如下所示：

此时，我们考虑一次重启：

1. 假设 $ac{t}_{12}\ge \lambda N$，可以发现 $z_{12}$ 需要与 $z_{16}$ 组成一个 2-comp，并且 $z_{16}$ 已经被生成，于是我们直接生成一个 2-comp($z_{12},z_{16},z_{27},z_{28}$)，使用 $z_{27}+z_{28}$ 替换 $z_{12}+z_{16}$ ，并生成 SAT 子句：

$$\begin{array}{rl}\neg z_{12}& \vee \neg z_{28}\\ \neg z_{16}& \vee \neg z_{28}\\ z_{12}\vee & z_{16}\vee \neg z_{27}\end{array}$$

2. 假设 $ac{t}_{18}\ge \lambda N$，但这时我们发现 $z_{20}$ 还没有被生成（因为需要构造出门 2-comp($z_{18},z_{20},z_{25},z_{26}$) ，于是，我们需要先生成 $z_{20}$，由于生成 $z_{20}$ 需要生成 $z_{14}$，经过向上的 dfs，我们最终获得集合为 $\{z_5,z_7,z_{15}\}$，最终，得到 $z_{20}$ 后，我们使用2-comp($z_{18},z_{20},z_{25},z_{26}$)，将 $z_{18}$ 进行替换，如下图所示：

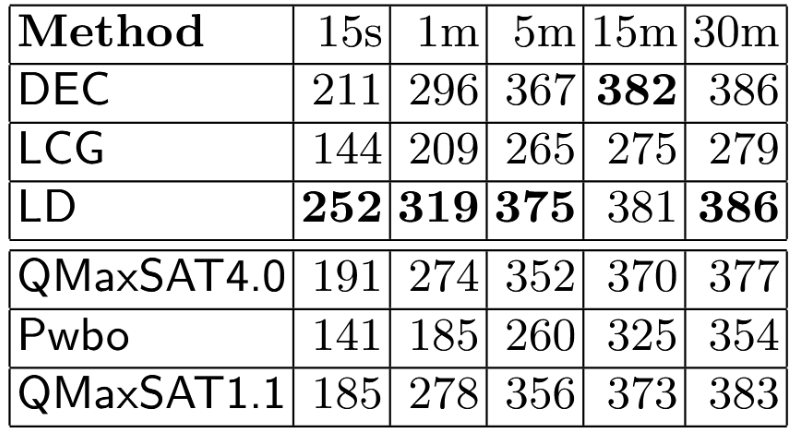
实验结果

Benchmark 选取大多为 SAT 问题带有一个基数约束形式的目标函数 $x_1+\cdots +x_n$，我们的做法是：

1. 首先，SAT 会给出初始问题的赋值 $O$

2. 接着，我们迭代使得 $O=O-1$，并在原有的子句约束上加入基数约束 $x_1+\cdots +x_n\le O$，直到在规定时间内找不到 SAT 的赋值

 Partial MaxSAT

数据来源于 MaxSAT Evaluation 2011，我们通过对所有软子句中加入一个新变量，将问题转化为 SAT 问题，并将目标函数设置为加入的新变量之和