RoundingSAT 阅读笔记

Tldr

文章链接

RoundingSAT 的工作可以看作者自己的网站：RoundingSAT，实验室名字也很有意思：MIAOresearch

Divide and Conquer: Towards Faster Pseudo-Boolean Solving

Abstract

The last 20 years have seen dramatic improvements in the performance of algorithms for Boolean satisfiability—so-called SAT solvers—and today conflict-driven clause learning (CDCL) solvers are routinely used in a wide range of application areas. One serious short-coming of CDCL, however, is that the underlying method of reasoning is quite weak. A tantalizing solution is to instead use stronger pseudo-Boolean (PB) reasoning, but so far the promise of exponential gains in performance has failed to materialize—the increased theoretical strength seems hard to harness algorithmically, and in many applications CDCL-based methods are still superior. We propose a modified approach to pseudo-Boolean solving based on division instead of the saturation rule used in [Chai and Kuehlmann ’05] and other PB solvers. In addition to resulting in a stronger conflict analysis, this also improves performance by keeping integer coefficient sizes down, and yields a very competitive solver as shown by the results in the PseudoBoolean Competitions 2015 and 2016.

简介

SAT 的局限性

CDCL 的推理（reasoning）能力差，因为其推理能力主要基于归结证明；以及其表达能力有限，只能解决以 CNF 形式表达的问题（虽然都可以规约，但会引入很多子句和变量），虽然有很多预处理技术（高斯消元，基数推理）可以提高很多速度，但这都与编码方式有很大关系，有时候并不是很有效果

由于 SAT 具有很大的局限性，于是，我们转向使用线性伪布尔约束来描述问题，这种约束形式能够表达比 CNF 更多的信息，但结构又与 CNF 很相似，于是基于 CNF 的技术可以应用到 PB 上

一些 PB 求解器仍然是基于归结的，这些求解器会将输入转化为 CNF，再进行求解；主要有两类做法：

1. eagerly：先转化为 CNF，然后直接调用 CDCL 求解器求解，代表是 MiniSat+，Open-WBO，NaPS
2. lazily：在修改的 CDCL 求解器中，保持输入的 PB 格式，但仅以子句的形式导出新的信息，代表为 Sat4j

另一种做法是使用切平面法来解决 PB 问题，但这种做法需要将 CDCL 框架拓展到 PB 上，这是十分困难的。

从理论的观点来看，使用切割平面似乎是很可取的，因为这种方法从来不比归结差，甚至可以做到指数级的更强。然而，实际上并非如此，通常基于 CDCL 的求解器优于基于切平面法的 PB 求解器。

在这篇文章中，提出了一个基于 CDCL 的 PB 求解器 RoundingSAT

基于冲突分析的 PB 求解

首先，我们回顾 PB 约束的标准形式：

$$\sum _i{c}_i\cdot l_i\ge w$$

其中，$l_i\in \{x_i,\neg x_i\}$, $x_i\in \{0,1\}$ ，而 $c_i,w\in {\mathbb{N}}_0^{+}$，将 $w$ 称为满足度（或者简称为度）

我们将部分真值赋值 $\rho$ 看作由 $\rho$ 设定为真的文字集合，也就是说如果 $l\in \rho$，那么 $\rho (l)=1$

一个传统的 CDCL 框架如下图所示：

在这里，我们不详细解释 CDCL 是如何工作的，我们希望做的是将 CDCL 中的两个重要部件引入到 PB 中来（重启与子句库之类的技术不在本文的探讨范围内）

单元传播

在 SAT 中，对于任意一条子句，只要有一个文字为真，子句即可为真，因此我们可以很轻松的进行单元传播，而在 PB 中，这种简单的成真条件不存在了，于是我们需要重新考虑传播的方案

首先，我们引入一个记号，对于任意一条约束 $C:={\sum }_i{c}_i\cdot l_i\ge w$：

$$slack(C,\rho )=\sum _{i:\rho (l_i)\ne 0}{c}_i-w$$

可以发现 $slack(C,\rho )$ 本质上表示，在给定赋值 $\rho$ 的条件下，当前约束的最大值与度的差距

显然当 $slack(C,\rho )<0$ 时，约束是不满足的，我们定义传播如下：

如果文字 $l_i$ 未被赋值，且有 $slack(C,\rho )<c_i$，那么我们称 $C$ 蕴含/传播了文字 $l_i$，也就是说除非将 $l_i$ 赋值为真，否则约束 $C$ 不成立

类比回 SAT

我们可以将文字的系数视为 $1$，那么子句的$slack=0$ 时，我们可以判定，文字 $l_i$ 一定为真（因为已经变成了一条单元子句）

存在的重要问题

显然，这里我们会发现一个很严重的问题，当约束不是子句时，我们更难有效的检测约束是否在传播（因为 $slack$ 的值不能期望只通过某一个文字为真就使其大于等于 0）

然而本文并不会详细探讨这个问题

冲突分析

分析的方法是使用广义归结来进行，其定义如下：

给定一对存在冲突的约束 $C:al+{\sum }_i{c}_i\cdot l_i\ge w$ 与约束 $C^{\prime }:b\overline{l}+{\sum }_i{c}_i^{\prime }\cdot l_i^{\prime }\ge w^{\prime }$，其在文字 $l$ 的赋值上有冲突，我们假定 $g=gcd(a,b)$，那么广义归结 $Res(C,C^{\prime },l)$ 定义为：

$$\frac{b}{g}\sum _i{c}_i\cdot l_i+\frac{a}{g}\sum _i{c}_i^{\prime }\cdot l_i^{\prime }\ge \frac{bw+a{w}^{\prime }-ab}{g}$$

SAT 中的归结

假定一对存在冲突的子句 $C\vee x,D\vee \overline{x}$，我们定义归结 $Res(C,D)$ 如下：$Res(C,D)=C\vee D$

一个简单的 PB 冲突例子

考虑 $C:2x_1+2x_2+2x_3\ge 3$, $C^{\prime }:\overline{x_1}+x_3\ge 1$，在 $x_1$ 上有冲突，于是 $Res(C,C^{\prime },x_1):2x_2+4x_3\ge 3$

随后，我们反复回退决策层，试图找到最早的那次冲突决策点，从而得到学习子句（这也是 CDCL 中 1UIP 的做法）

存在的问题

我们考虑以下例子，$C:2x_1+3\overline{x_2}+x_3\ge 3$，$C^{\prime }:4x_2+4x_3+2x_4+x_5\ge 4$，假定，我们的决策序为 $x_4=1,x_3=0$，此时 trail 中的文字为 $x_4,\overline{x_3}$

随后，在单元传播时，我们会在 $C$ 中考虑传播 $\overline{x_2}$ ，trail 变为 $x_4,\overline{x_3},\overline{x_2}$，但此时 $C^{\prime }$ 发生冲突，我们需要进行冲突分析，根据前文，我们得到 $Res(C,C^{\prime },\overline{x_2}):8x_1+16x_3+6x_4+3x_5\ge 12$，然而这个约束直接将 trail 中 $x_4,\overline{x_3}$ 的赋值全违反了，此时我们得到的学习子句（学习约束？）就没有任何意义了

弱化与饱和

我们通过两个算子，$weaken$ 与 $saturate$ 来解决这个问题

弱化

$weaken$ 从约束中删除一个文字，并从度中减去它的系数

例如对于约束 $C:x_1+2x_2+3x_3\ge 4$ ，我们考虑对 $x_1$ 做弱化操作 $weaken(C,x_1)=2x_2+3x_3\ge 3$

可以发现，弱化操作就是直接将某个文字的取值假定为真

饱和

$saturate$ 将约束中所有系数的大小降低到刚好不满足约束的程度，形式化的写为 $saturate(C):{\sum }_i\min (c_i,w)\cdot l_i\ge w$

例如对于约束 $C:x_1+2x_2+3x_3\ge 4$ ，$saturate(C)=x_1+2x_2+2x_3\ge 4$

最终的冲突分析

于是，最终的冲突分析如下所示：

一个简单的分析示例

考虑两个约束 $C:2x_1+2x_2+2x_3+2x_4+x_5\ge 6,C^{\prime }:2\overline{x_1}+2\overline{x_2}+2\overline{x_3}+2\overline{x_4}\ge 3$，我们可以发现，这两条约束本质上是两条基数约束：$x_1+x_2+x_3+x_4\ge 3,\overline{x_1}+\overline{x_2}+\overline{x_3}+\overline{x_4}\ge 2$，这两条基数约束显然是矛盾的，不过算法没办法立刻发现这个问题

假设此时的 trail 为 $\rho =(\overline{x_1}/d,x_2/C,x_3/C,x_4/C)$，此时，我们发现 $C^{\prime }$ 不满足，于是我们进行冲突分析（其中，冲突约束为 $C^{\prime }$，原因约束为 $C$）

1. 对于 trail 中的最后一个文字，我们有 $Res(C^{\prime },C,\overline{x_4}):x_5\ge 1$，其 $slack\ge 0$，于是我们进行归结
2. 我们在原因约束中选择一个不同于 $x_4$ 的不导致冲突的文字，例如 $x_2$，接着我们做弱化与饱和操作，得到新的原因约束：$2x_1+2x_3+2x_4+x_5\ge 4$，其中饱和操作没有任何影响，因为 $\overline{x_1}$ 为真
3. 接着，我们得到新一轮的归结 $Res(C^{\prime },2x_1+2x_3+2x_4+x_5\ge 4,\overline{x_4})=2\overline{x_2}+x_5\ge 1$，此归结的 $slack\ge 0$，于是我们继续进行归结
4. 下一个被选择的文字为 $x_3$，我们得到新的原因约束为 $2x_1+2x_4+x_5\ge 2$，此时归结的 $Res(C^{\prime },2x_1,+2x_4+x_4\ge 2,\overline{x_4})=2\overline{x_2}+2\overline{x_3}+x_5\ge 1$，其 $slack\ge 0$，于是继续归结
5. 下一个被选择的为 $x_5$，得到新的原因约束为 $x_1+x_4\ge 1$，于是归结为 $Res(C^{\prime },x_1+x_4\ge 1,\overline{x_4})=2\overline{x_2}+2\overline{x_3}\ge 1$，此时的 $slack=-1$，结束循环

最终，我们得到的 $C_{reason}=x_1+x_4\ge 1$

值得注意的是，我们并没有真正的计算 $slack(C+C^{\prime },\rho )$ 的值，我们通过使用上界来近似计算，以获得更好的效率：

$$slack(C+C^{\prime },\rho )\le slack(C,\rho )+slack(C^{\prime },\rho )$$

基于 Division 的冲突分析

我们将饱和算子替换为分割算子，其工作原理如下所示：

$$divide(C,d):\sum _i\lceil c_i/d\rceil \cdot l_i\ge \lceil w/d\rceil$$

其中 $d\in {\mathbb{N}}_0^{+}$

RoundToOne

首先外面介绍一个组件算法，RoundToOne，其流程如下图所示：

其接受一条约束 $C$，一个文字 $l$ 以及当前的 trail $\rho$ 为参数，输出一条约束 $C^{\prime }$，这条约束是将 $C$ 在 $l$ 上的舍入（这里称为 rounding），且 $l$ 的系数为 $1$，约束 $C^{\prime }$ 还有一个额外的性质：

对于任意 trail $\rho$ 和任意 PB 约束 $C:{\sum }_i{c}_i\cdot l_i\ge w$，对于文字 $l_i$ 我们有如下性质成立：

$$slack(\text{roundingToOne}(C,l_i,\rho ),\rho )=\lfloor slack(C,\rho )/c_i\rfloor$$

于是，我们有推论：

若一条约束 $C:{\sum }_i{c}_i\cdot l_i\ge w$ 是一条未违背的约束，且其在赋值为 $\rho$ 的条件下传播了文字 $l_i$，即 $0\le slack(C,\rho )\le c_i$，那么我们有 $slack(\text{roundingToOne}(C,l_i,\rho ),\rho )=0$，否则，如果 $slack(C,\rho )<0$，那么 $slack(\text{roundingToOne}(C,l_i,\rho ),\rho )<0$

RoundToOne 的示例

考虑两个约束 $C:2x_1+2x_2+2x_3+2x_4+x_5\ge 6,C^{\prime }:2\overline{x_1}+2\overline{x_2}+2\overline{x_3}+2\overline{x_4}\ge 3$，假设此时的 trail 为 $\rho =(\overline{x_1}/d,x_2/C,x_3/C,x_4/C)$，此时，我们发现 $C^{\prime }$ 不满足，于是我们进行冲突分析（其中，冲突约束为 $C^{\prime }$，原因约束为 $C$）

1. 我们求得 $x_4$ 的系数为 $c=2$，随后开始迭代
2. 由于 $x_2,\dots ,x_5$ 均不是成假的，因此我们进入第二步判断，而由于只有 $x_5$ 的系数无法整除 $c$，于是，$x_5$ 被弱化，我们得到了约束 $C:2x_1+2x_2+2x_3+2x_4\ge 5$，此时循环结束
3. 最后，我们通过分割算子得到了以下约束：$C:x_1+x_2+x_3+x_4\ge 3$

此时，我们得到了一个比原来的方案更强的约束（原来的约束为 $x_1+x_4\ge 1$）

RoundToOne 的变形

考虑 $C:2x_1+3x_3+3x_3+3x_4\ge 8$，此时我们在 $rho=(x_1,x_2,x_3,\overline{x_4})$ 的情况下对 $x_1$ 做舍入，我们将会得到约束 $x_1+2x_4\ge 1$

但如果我们不在一次执行让所有满足条件的文字弱化，而是让算法每次在某一个文字上弱化，并且在分割后的 $slack=0$ 时终止，那么我们就可以得到更强的约束 $x_1+2x_2+2x_4\ge 3$

然而，可以证明，无论进行弱化的顺序如何，这种迭代方法总是会弱化几乎和 roundToOne 一样多的文字；更准确地说，区别至多是 $c-1$ 个文字，其中 $c$ 是除数

另一种变形是在文字上做部分弱化，例如，从 $C$ 中导出 $2x_1+2x_2+2x_3+3x_4\ge 6$，随后，分割得到 $x_1+x_2+x_3+2x_4\ge 3$

RoundingSAT 冲突分析

我们的冲突分析算法如下所示：

PB 冲突分析中存在一些特殊情况，使其比 CDCL 更加复杂

1. 一个归结操作可能会取消当前决策层的所有赋假文字，在这种情况下，分析可能会继续到更早的决策层，甚至可能发生冲突分析能够进行到最高决策层，从而推导出实例是不可满足的

2. 学习到的约束可能在其断言（激活）级别¹被违反，在这种情况下，在调用单元传播之前会重复执行冲突分析。

跳过解析步骤

与 CDCL 冲突分析的另一个有趣对比是，如果  $slack(C_{confl},\rho )$  的值非常负，那么可能可以忽略与  $C_{reason}$​  的解析步骤，直接从赋值序列  $\rho$  中移除被传播的文字  $l$，同时仍然保持不变量  $slack(C_{confl},\rho -l)$。

直观上，这似乎可以导致一种更紧凑的分析，仅涉及冲突真正需要的原因，从而可能产生更好的学习约束。然而，当我们通过实验评估这一想法时，结果并未改善，因此最终我们没有采用这一方法。尽管如此，这仍然是一个值得进一步探索的有趣观察。

实验

这部分，对比了算法：

1. Sat4j
2. Open-WBO
3. Sat4jRes+CP（使用了切平面法的 Sat4j）

Benchmark 为 PB 竞赛的例子，分类为 DEC-SMALLINT-LIN

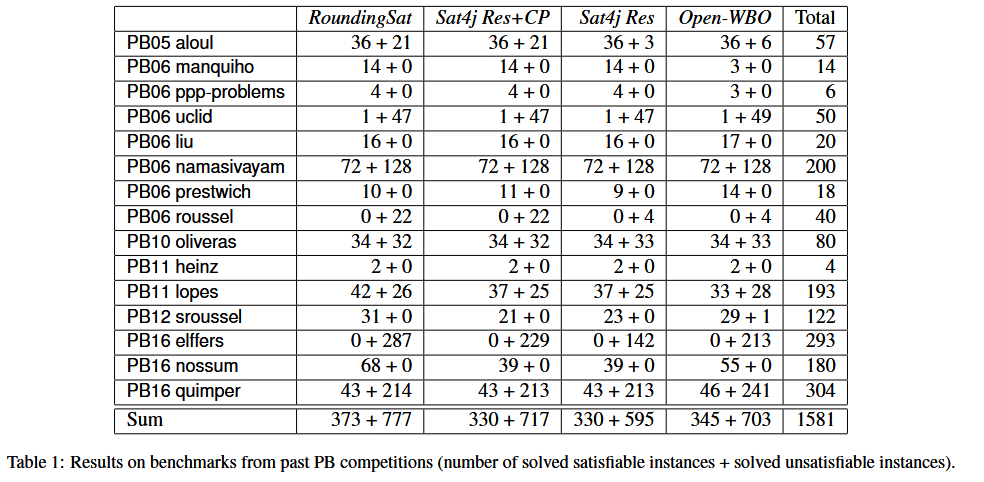
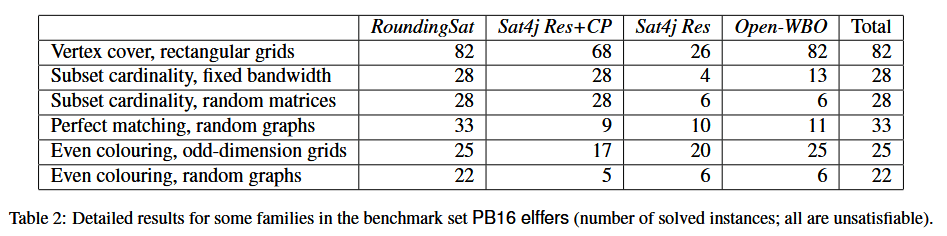
结果如下图所示：

未来工作

一个明显方向是进一步改进我们的求解器。与其他伪布尔求解器一样，RoundingSat 对输入格式很敏感，在 CNF 公式上表现很差。

解决这一问题的一种方法是在可能的情况下将 CNF 重写为更有效的线性约束的规则；特别地，一个重要的挑战是对编码基数约束的子句集合进行 基数检测 AAAI’20

Remarque

1. 断言级别（Assertion Level）  是冲突驱动子句学习（CDCL）SAT 求解器中的一个重要概念，用于描述在搜索过程中某个约束（或子句）被“断言”或“激活”的决策级别。它表示在搜索树的某个特定层次上，某个约束开始对当前的变量赋值产生影响。 ↩