基数约束SAT的精确求解器

Tldr

文章链接

From Clauses to Klauses

Abstract

Satisfiability (SAT) solvers have been using the same input format for decades: a formula in conjunctive normal form. Cardinality constraints appear frequently in problem descriptions: over 64% of the SAT Competition formulas contain at least one cardinality constraint, while over 17% contain many large cardinality constraints. Allowing general cardinality constraints as input would simplify encodings and enable the solver to handle constraints natively or to encode them using different (and possibly dynamically changing) clausal forms. We modify the modern SAT solver CADICAL to handle cardinality constraints natively. Unlike the stronger cardinality reasoning in pseudo-Boolean (PB) or other systems, our incremental approach with cardinality-based propagation requires only moderate changes to a SAT solver, preserves the ability to run important inprocessing techniques, and is easily combined with existing proofproducing and validation tools. Our experimental evaluation on SAT Competition formulas shows our solver configurations with cardinality support consistently outperform other SAT and PB solvers.

Introduction

对于基数约束而言，即使存在 PB 求解器，其推理能力比 SAT 求解器更强，但与 SMT 中字符串和位向量的理论类似，通常需要一种将基数约束转化为子句的 Eager 方法，然后调用 SAT 求解器。

Related Work

为了提高求解器在处理具有基数约束问题时的性能，研究者们主要从三个方面入手：增强底层证明系统、改进编码方式，或者直接在约束上进行原生传播。求解器可以利用更强的证明系统，无论是处理具有更丰富输入结构的公式，还是处理 CNF（合取范式）中的公式。例如，求解器 RoundingSAT 利用了切平面的优势，使其能够高效解决一些对归结法来说较为困难的问题。求解器 SAT4J 在预处理步骤中实现了基数提取 和广义归结，从而能够快速解决包含基数约束的 CNF 公式，并且还提供了对寻找哈密顿环的原生处理支持。此外，为了简化公式的编写，求解器工程师们还提供了对基于基数表示的支持。例如，求解器 MINISAT+ 支持基于基数的输入，并将公式转换为子句，而求解器包 PYSAT 则提供了将约束转换为子句的 API 调用。最后，求解器 MiniCARD 通过原生处理基数约束，显著减少了内存占用并改进了传播性能。

然而，最近的研究大多集中在更强的证明系统或更好的编码方式上。这部分是因为基数约束传播的实现细节在现代内处理技术发展之前就已经出现，且没有考虑到证明生成，并且仅在一些手工构造的公式上进行了评估。我们在现代 CDCL（冲突驱动子句学习）的背景下重新审视了原生基数约束处理，展示了在某些问题上，性能可以在不损害验证工具链的情况下得到提升（假设不使用切割平面）。

At-Least-K Conjunctive Normal Form

由于所有的基数约束都可以统一转变为 “至少”，在 Conflict Directed Lazy Decomposition 中有基数约束及其转变的介绍。于是，在这里我们只考虑 “至少” 类型的约束，我们称为 conjunction of klauses ，简称 KNF 。

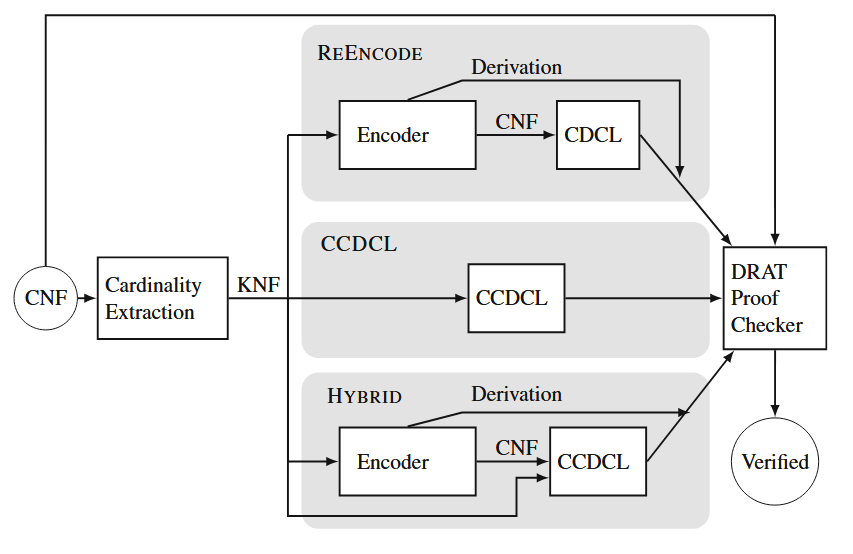
我们的总体框架如上图所示，对于一个从 CNF 变化得到的 KNF，我们有三种独立的求解器来求解：REENCODE, CCDCL, HYBRID。每种配置都会产生一个 DRAT 证明（或者说是 SAT 赋值）

1. REENCODE 通过将基数约束编码为子句（CNF）的形式，然后调用 CDCL 求解器进行求解，然而由于 CDCL 求解器使用的是原 CNF 公式中没有出现的重新编码的子句，因此对于子句重编码的 DRAT 推导必须先于求解器的 DRAT 证明。
2. CCDCL 通过在 klauses 上直接传播求解 KNF。如果提取的约束是弧相容¹的(否则增加推导过程即可)，则 CCDCL 求解器生成的 DRAT 证明可以通过输入的 CNF 公式进行验证。
3. HYBRID 通过混合上面两种方法，CCDCL 由于是一个向下兼容的求解器，其也可以求解 CNF 公式，于是，其接收了重新编码后的 CNF 与原来的 KNF 作为输入，注意，重新编码的 CNF 会作为冗余公式存在与求解器中，而 klauses 只在 SAT 的模式下被观察并传播，因此，当求解器以 UNSAT 模式在基数约束上传播时，它仅使用重新编码的子句。这使得求解器可以访问编码内的辅助变量，而这些变量对于寻找不可满足公式的简短证明是极其重要的。当求解器处于 SAT 模式时，它可以在 klauses 上直接传播，从而允许绕过辅助变量的更快传播。

三种不同的求解方法凸显了 KNF 格式所提供的灵活性。在某些情况下，对 klauses 的较小表示和快速传播是有益的。在其他情况下，重编码 klauses 引入辅助变量可以导致更短的证明。而两种方法的结合可能对未知问题效果最好。

Cardinality Constraint Extraction and Analysis

从 CNF 中提取 KNF

这里，我们实现了自己的预处理器，通过探测 CNF 中的基数约束，并将 CNF 转化为 KNF

具有成对约束的 AMO 约束可以通过寻找图中的团来检测，其中，图由文字作为顶点，二元子句中文字之间的关系为边构成。虽然寻找最大团是 NP 难的，但是简单的贪心方法可以很好地完成这个任务。

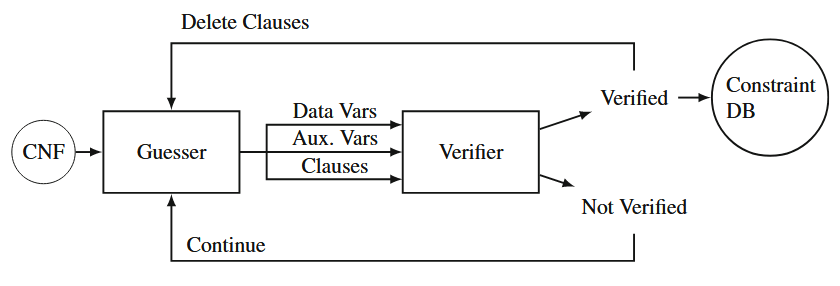
我们通过一个名为 guess-and-verify 的算法来探测那些非成对的约束，算法的流程如下图所示：

我们的猜测方法旨在从 CNF 表示的子句中寻找可能隐含基数约束的模式，并将这些子句中的变量分类为 数据变量 或辅助变量。具体步骤如下：

1. 变量极性分析：首先，该方法检查公式中的所有二元子句，并根据变量的极性将其分类为：
   • 单极性变量（Unate）：始终以同一极性出现（例如，变量在子句中只以正文字或只以负文字形式出现）。
   • 双极性变量（Binate）：在子句中同时以正文字和负文字形式出现。
2. 变量角色假设：
   • 数据变量：假设为单极性变量（即仅以一种极性参与约束）。
   • 辅助变量：必须是双极性变量（通常用于编码基数约束的逻辑结构）。
3. 传递闭包构建：从某个双极性变量出发，提取器会构建一个 传递闭包，包含所有与该变量在同一子句中出现的其他双极性变量。这一过程递归扩展，直到覆盖所有相关联的双极性变量。
4. 数据变量选择：在最终形成的闭包集合中，选择所有与此闭包相关子句中的单极性变量作为 数据变量。

这些单极性变量被认为是基数约束的实际参与变量，而双极性变量则是编码过程中引入的辅助变量。

我们发现，这种基于变量极性猜测的方法能够有效检测  At-Most-One 约束的标准编码形式，包括先前提取工具处理的所有情况。然而，该方法在以下场景中可能失效：

1. 当某个数据变量在不同的约束中以不同极性（例如，在某个约束中仅以正文字出现，而在另一个约束中以负文字出现）时，该变量可能被错误分类。
2. 某些子句模式可能满足极性条件（如单极性或双极性变量的组合），但实际并不编码基数约束。

尽管存在上述问题，但这些误提取的模式会在后续的 Verifier 中被拒绝。当前验证器可以判断一组子句是否编码了  非 AMO 的基数约束（例如“恰好一个”或“至少两个”），但我们尚未找到一种可靠策略，能够从整个 CNF 文件中区分这些子句与其他无关子句。

Future Work

我们计划将提取能力扩展到通用的基数约束

基于 BDD 的分析验证

为什么使用 BDD 的一些猜测

The full potential for efficient algorithms based on the data structure was investigated by Randal Bryant at Carnegie Mellon University: his key extensions were to use a fixed variable ordering (for canonical representation) and shared sub-graphs (for compression).

本文第三作者就是 Randal Bryant

我们使用基于 BDD 的分析来验证我们 上文中 猜测的基数约束实际上是基数约束

Todo

算法需要补全

Cardinality Conflict-Driven Clause Learning

当我们得到 KNF 后，我们在这里引入 CDCL 的带基数传播的拓展 CDCL。对于具有许多大 klauses 的问题，CCDCL 会进行简单化简处理，降低公式的规模，并提高基数约束传播的速度。

对于以下例子：

$$\begin{array}{rl}{K}_1:x_1+x_2+x_3+\neg x_4+x_5& \ge 3\\ C_1:x_1+x_2+x_3+\neg x_4+x_5& \ge 1\end{array}$$

假设部分赋值 $\neg x_1\neg x_2$ 在 $K_1$ 中传播后，得到赋值 $x_3\neg x_4{x}_5$ ；而部分赋值 $\neg x_1\neg x_2\neg x_3{x}_4$ 在 $C_1$ 中传播，得到赋值 $x_5$，我们发现 $K_1$ 可以一次性传播三个赋值，而 $C_1$ 只能传播一个，因此基数约束在传播能力上比传统子句更强。

CCDCL 存在以下权衡：

1. 某些内处理技术（如子句简化、变量替换或冗余约束删除）需要被限制或禁用，因为它们可能与基数约束的原生处理逻辑冲突。例如，删除看似冗余的辅助变量可能会破坏基数约束的结构完整性。
2. 支持基数约束的传播和冲突分析算法会显著复杂化。例如，在冲突分析中需额外处理基数约束的逻辑依赖关系，而非单纯基于子句的蕴含。
3. 在子句编码中引入的辅助变量可能对学习有用子句至关重要。例如，辅助变量可能隐含某些关键逻辑关系，若被忽略或简化，可能导致冲突子句的质量下降，进而影响搜索效率。

一些技术细节

一个 klause 需要 $k+1$ 个观察字，而一般的子句只需要两个观察字，如下图所示：

传播算法

对于一个 klause，假定其一个观察字 $w_i$ 被赋值为 $\neg l_i$，那么第一个未被赋值/满足序数为 $l_{k+2}$ 的文字就会与 $l_i$ 交换位置，此时 $w_i$ 被释放，然后一个新的观察字 $w_{k+2}$ 被创建（用以观察 $l_{k+2}$）。如果不存在这样的一个文字 $l_{k+2}$，那么此时 $l_1,\dots ,l_{k+1}$(不包括 $l_i$) 均被赋值为真，其赋值原因被设置为 $l_i,l_{k+2},\dots ,l_s$ 均为假。如果任何一个想要传播的文字已经被赋值为假，那么就会发生冲突，传播算法就会失效。冲突子句包含原因文字，$l_i$，以及除 $l_i$ 外第一个被赋值为假的观察字。

冲突分析

冲突分析和 CDCL 中的一致，从冲突子句向后遍历蕴涵图到第一个唯一蕴涵点，以产生学习子句。其中蕴涵图用于捕获决策或传播的文字的顺序和依赖关系，其中每个顶点是赋值为真的文字，顶点的入边为原因文字，其表明了该文字为什么被传播（决策文字没有入边）。直观地说，CDCL 学习到的子句是 RUP (Reverse unit propation) 的，因为它们代表蕴涵图中的一个割，从这个割出发，单元传播会产生冲突。

在 CCDCL 中，考虑一个被 klause 传播的文字，在依赖图中，其原因文字显然是 klause 那些已经被传播的文字。由于蕴含图的重要性质没有变化，因此我们可以使用子句最小化来生成学习子句，假设学习到冲突子句  $C=(\neg x_1\vee \neg x_2\vee x_3)$，若通过分析发现  $x_3$​  的赋值不依赖  $x_1$，则可删除  $\neg x_1$，简化为  $C^{\prime }=(\neg x_2\vee x_3)$。

然而，我们并没有考虑 klauses 在时间回溯(Chronological Backtracking) 中的影响，因此我们暂时只允许使用回跳技术。

Future Work

CCDCL 如何支持 Chronological Backtracking

其他细节

这里我们介绍一些有作用的且较为重要的 SAT 求解技术，而为了支持这些技术，我们将 klause 的子句库划分为 clause 与 klause 的类型。

1. 当一个子句是另一个子句的子集时，它可以覆盖(或替换)另一个子句。
2. 对于所有没有出现在 klause 中的变量，我们允许进行 BVE 操作¹
3. 子句重激活²
4. 我们在相位保存的阶段使用局部搜索，一个成假的基数约束为一个文字的 break 值增加了额外的权重，这取决于基数约束中包含了多少个伪造的文字。

Future Work

实现更多的策略：failed literal probing 与 Equivalent Literal Substitution

证明检查

Fix

实验

单个设备为 128 核 256 G 的机器，我们在集群上并行测试，每个节点跑 64 个实验，每个节点的时限设置为 5000 s，因此每个进程平均能够分配到内存为 4 G。

我们测试的对比算法与输入格式如下图：

Benchmark 设置为 SAT 竞赛的例子与两个实际问题，我们将其编码为 CNF 的形式。

我们引入 PAR-2 来作为求解器之间比较的指标，其定义为 超时次数和内存超限次数相加并加上完整运行时间之和，再乘以 2 倍的时限(10000)，再对某一求解器求解的公式数取平均。 PAR-2 越小，求解器的性能越好。

SAT Competition Benchmarks

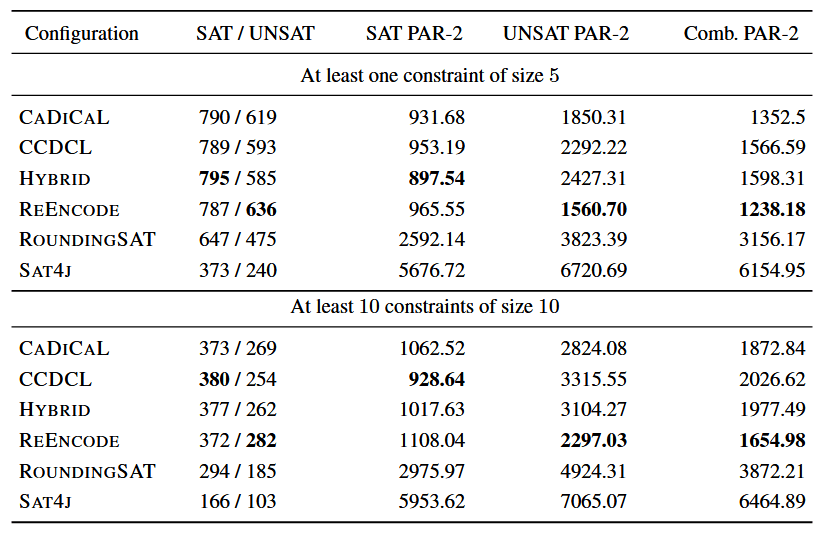
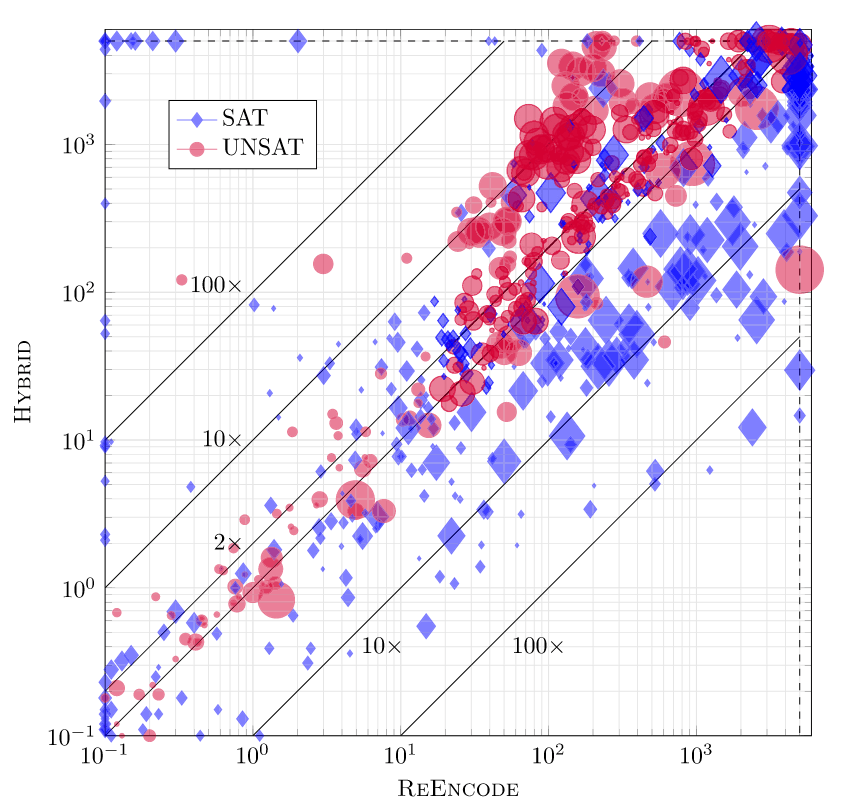
结果如下图所示：

下图展示了基于基数的传播和编码之间的权衡。HYBRID 实现了模式转换，在基于基数的传播之间进行了大约一半的时间，导致求解不可满足公式的平均速度减慢。

Magic Squares and Max Squares

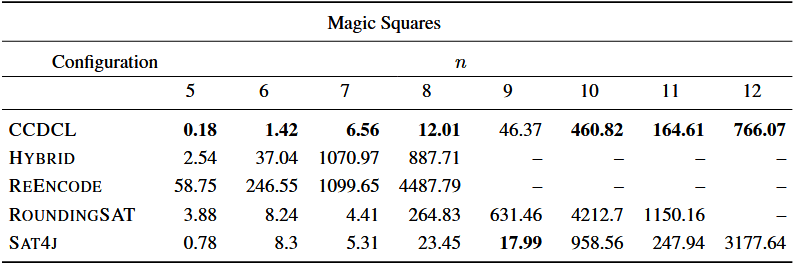
幻方(Magic Squares) 问题的定义较为简单，其编码后本质上可以看作是一个 PB 问题，其含有的基数约束较多，而子句约束较少，实验表现如下：

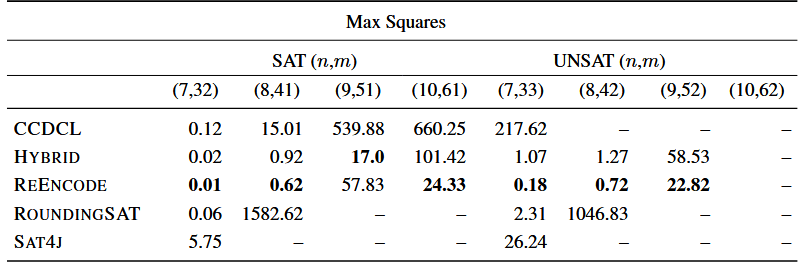
Max Squares 问题的定义为是否存在一种染色方案，在 $n\times n$ 的网格中，将 $m$ 个格子染为黑色后，使得不存在任意四个黑色格子能够组成正方形的四个角。这里，我们使用四个文字的子句来约束任意一个正方形的四个角均不为黑色，使用一个 klause 来约束至少由 $m$ 个格子为黑色。

实验表现如下：

对于这个问题，基于基数的传播和 PB 推理都是无效的。这个问题的独特之处在于它包含一个大的基数约束，而不是 Magic Squares 包含许多基数约束。这可能解释了即使是可满足公式，CCDCL 的性能也会变差。

Tip

这里的 HYBIRD 似乎可以和 Conflict Directed Lazy Decomposition 的方法联系起来，不知道效果会怎么样

Future Work

除了上文中提到的一些，还有如何通过 KNF 来提高局部搜索与并行求解的可能性。

Remarque

1. https://fmv.jku.at/papers/EenBiere-SAT05.pdf ↩ ↩²

2. https://arxiv.org/pdf/1807.11061 ↩