LS-PBO 阅读笔记

Tldr

文章链接

提出了一种局部搜索求解 PBO 的框架，主要的思路就是把优化转为判定，由此可以使用 SAT 局部搜索求解器的思路，通过对约束加权（惩罚值），并由此进行打分函数的设计，从而指导启发式算法工作

本文¹后续的改进版有：DeciLS-PBO FCS’23， NuPBO CP’23，ParLS-PBO CP’24

Efficient Local Search for Pseudo Boolean Optimization

Abstract

Pseudo-Boolean Optimization (PBO) can be used to model many combinatorial optimization problems. PBO instances encoded from real-world applications are often large and difficult to solve; in many cases, close-to-optimal solutions are useful and can be found reasonably efficiently, using incomplete algorithms. Interestingly, local search algorithms, which are known to be effective for solving many other combinatorial optimization problems, have been rarely considered in the context of PBO. In this paper, we are introducing a new and surprisingly effective local search algorithm, LS-PBO, for PBO. LS-PBO adopts a well designed weighting scheme and a new scoring function. We compare LSPBO with previous PBO solvers and with solvers for related problems, including MaxSAT, Extended CNF and Integer Linear Programming (ILP). We report results on three real-world application benchmarks, from the Minimum-Width Confidence Band, Wireless Sensor Network Optimization and Seating Arrangement Problems, as well as on benchmarks from the most recent PB Competition. These results demonstrate that our LS-PBO algorithm achieves much better performance than previous state-of-the-art solvers on real-world benchmarks.

PBO 问题简介

首先，我们介绍什么是 PBO 问题：给定一个变量集合 $X=\{x_1,\dots ,x_n\}$，其中 $x_i\in \{0,1\}$，问题定义为：

$$\begin{array}{rl}\underset{X}{\min }& c_i\cdot l_i\\ s.t.& \underset{j=1}{\overset{m}{\bigwedge }}\sum _{i=1}^n{a}_{ij}\cdot l_i\ge k_i\end{array}$$

其中，$l_i\in \{x_i,\neg x_i\},c_i,a_{ij},k_i\in \mathbb{R}$

Related Work

解决 PBO 的算法主要分为三类：

1. 基于 CDCL 的 SAT 求解器，代表为 OpenWBO，RoundingSAT，HYBRID
2. 分支限界法（BnB）
3. 不完备的局部搜索算法

在本文之前，唯一一篇提到使用局部搜索做 PBO 的文章为 ECNF ，本文提出一个名为 LS-PBO 的框架，在这个框架中，我们将 “目标函数”（objective function）变更为“目标约束”（objective constraints）， 将目标约束加入到 PBO 实例中。为了区分目标约束与原约束，我们引入了 Constraint Weighting Scheme 技术，与 Score Function 结合，指导局部搜索的进行

Constraint Weighting Scheme

对于一个给定的 PBO 问题：

$$\min \sum _{i=1}^n{c}_i\cdot l_i$$

我们考虑以下约束：

$$\sum _{i=1}^n{c}_i\cdot l_i<ob{j}^{\ast }$$

其中，$ob{j}^{\ast }$ 表示本次搜索时找到的最优解的目标函数值，在最开始时，$ob{j}^{\ast }=\infty$，于是，我们将一个优化问题转化为了判定问题

在此基础上，我们定义两个值：

1. 约束 $c:={\sum }_{i=1}^n{a}_i\cdot l_i▹k$ 的影响系数：$coeff(c):={\sum }_{i=1}^n\frac{a_i}{n}$
2. 对于一个 PBO 实例，约束的平均影响系数：$avgcoeff:=\frac{1}{m}{\sum }_{c=1}^{m}w(c)\cdot coeff(c)$

于是，我们的加权方案定义如下：

对于每个约束 $c$，我们首先初始化一个权重 $w(c)=1$，当搜索卡在局部最优时，我们更新约束的权重：

• 对于每个未满足的硬约束：$w(c)=w(c)+1$
• 对于目标约束，如果当前目标约束未满足且 $w(oc)\cdot coeff(oc)-avgcoeff\le \zeta$，那么 $w(oc)=w(oc)+1$

注意到，我们的主要目标是找到一个可行解。只有找到一个可行解，才认为优化是有意义的，因此，硬约束的权重应与目标约束的权重区别对待

直观地讲，为了找到一个可行解，目标约束的权重与硬约束的权重的差距不应该太大，否则，搜索很可能会被限制在满足目标约束的分配的子空间中。为了防止这种情况，在我们的加权方案中，我们对目标约束的权重设置了一个上限

Score Function

局部搜索算法通常使用一个打分函数与基于它的启发式来指导搜索过程。对于 SAT 及相关问题，这些打分函数通常衡量翻转一个变量的优势。在这里，我们定义了三个基于约束权重的打分函数

具体来说，我们定义了一个衡量满足硬约束的收益的得分函数和一个关于目标得分的得分函数，并考虑将这两个函数的和作为一个组合评分函数，首先，我们介绍约束的惩罚值

1. 如果一个硬约束未被满足，那么会带来 $w(c)\cdot (k-\sum a_i\cdot l_i)$ 的惩罚值
2. 无论目标约束是否满足，其一定带有 $w(oc)\cdot \sum c_i\cdot l_i$ 的惩罚值

于是，我们定义的评分函数如下：

• $hscore(x)$ 表示翻转 $x$ 后，硬约束惩罚值的下降值
• $oscore(x)$ 表示翻转 $x$ 后，目标约束惩罚值的下降值

将其组合后，得到：

$$score(x):=hscore(x)+oscore(x)$$

Framework

于是，一个简单的局部搜索框架如下图所示：

我们每次从 $score(x)>0$ 的变量集合中选取一个分数最高的进行翻转

如果这个集合为空，那么说明此时我们已经到达一个局部最优，于是，我们通过上文提到的权重分配策略，更新约束的权重，并通过随机扰动来跳出局部最优

Hint

注意，这里我们会优先选择构造出一个可行解，因此首先判断硬子句的满足情况

Experiments

参数的设置如下：

Params	$\zeta$
Value	10, 20, 50, 80, 100, 150, 200, 500

默认设置为 $100$，此时表现最好

对比的算法为：

• Open-WBO
• HYBRID
• Loandra
• SATLike-c
• LS-ECNF
• Gurobi

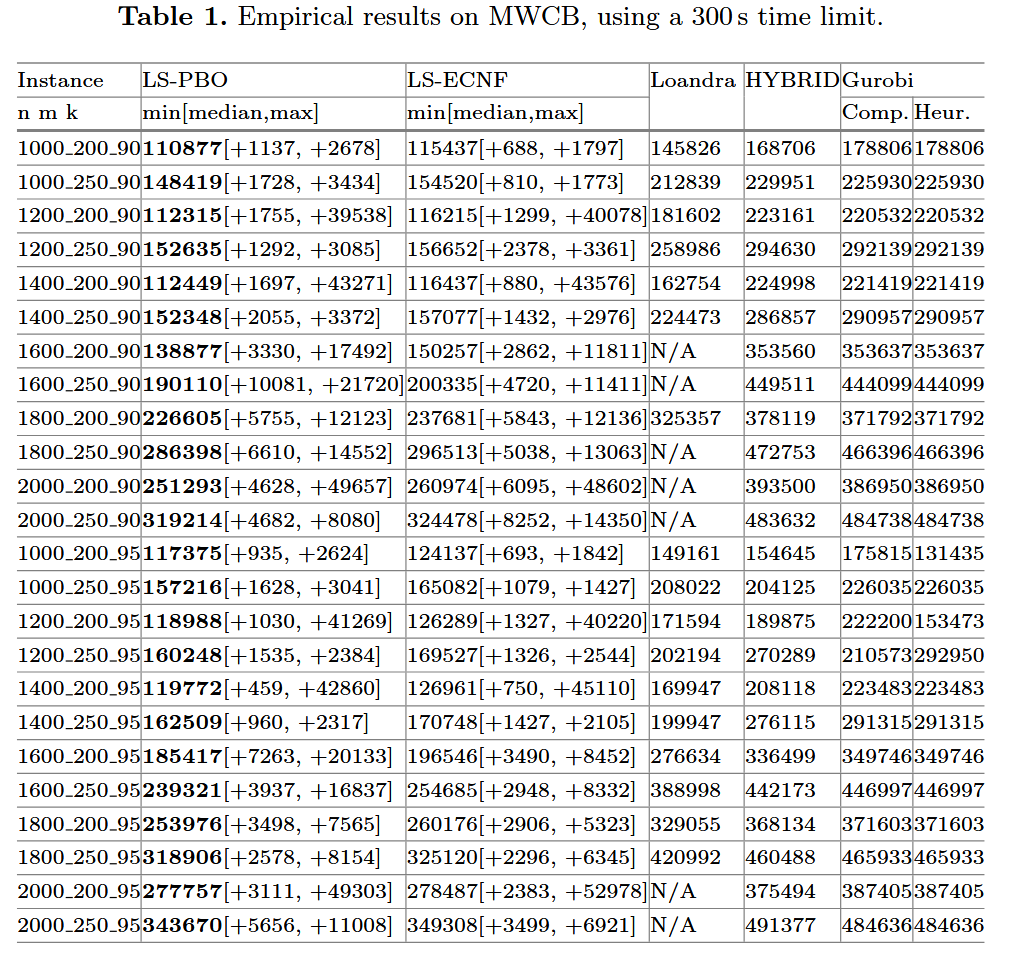
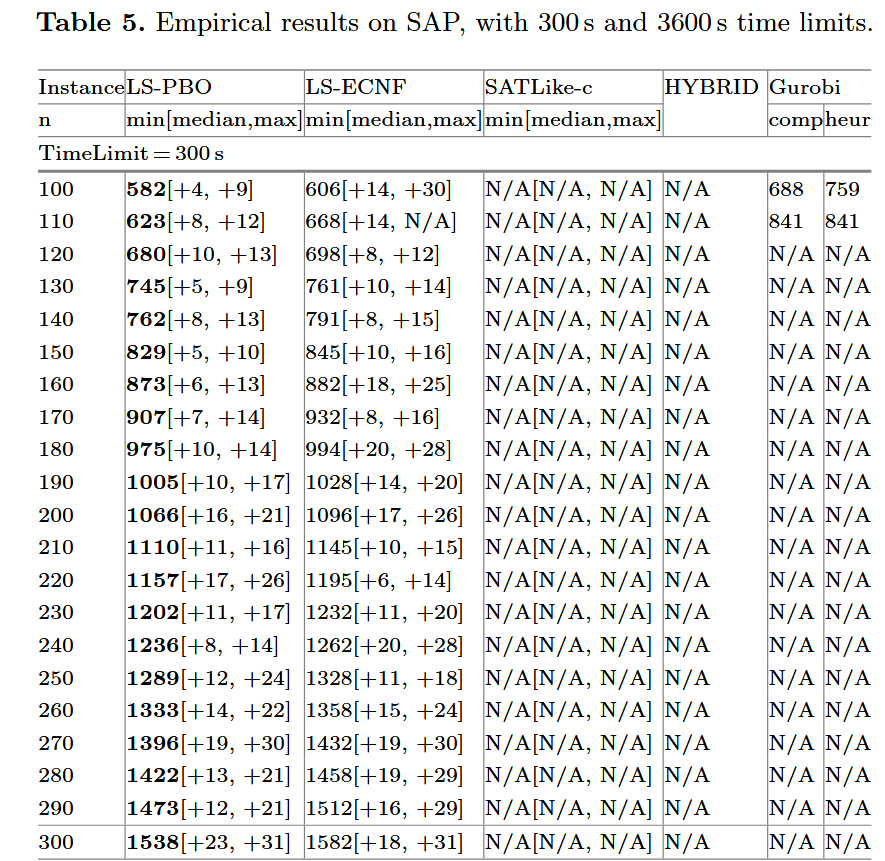
Benchmark 为 PB competition 中的例子

每个实例都会用不同的随机种子，运行 20 次，获得最大值，最小值，中位数与平均值

可以发现在这些问题上，LS-PBO 的效果都很好（时间限制只有 300s）

Remarque

1. 这其实是一个连载的系列，本文和后续的改进都是 Prof. Shaowei Cai 组的，不过中间有一个 DeciLS-PBO 不是蔡老师组的工作 ↩