NuPBO 阅读笔记

Tldr

文章链接

在本工作中，我们重点关注提高 SLS 求解 PBO 的性能。特别地，我们提出了两个主要的想法：

1. 一种新颖的评分函数，它考虑了未满足约束的违反程度，并利用一个平滑函数来平衡不同约束的违反程度。对于每个约束，其光滑函数被实例化为对应约束中出现的所有变量的系数的平均值
2. 一种新颖的 PBO 加权方案，我们不设置目标函数权重的上界，而是采用条件更严格的加权方案更新目标函数的权重

在 3 个 Benchmark 上，NuPBO 取得了比 LS-PBO 更好的性能，并且明显优于其他求解器。在其他 3 个 Benchmark 上，NuPBO 展现了其与其他求解器，尤其是 Gurobi 均有竞争能力

文章后续的改进有 ParLS-PBO CP’24

Towards More Efficient Local Search for Pseudo-Boolean Optimization

Abstract

Pseudo-Boolean (PB) constraints are highly expressive, and many combinatorial optimization problems can be modeled using pseudo-Boolean optimization (PBO). It is recognized that stochastic local search (SLS) is a powerful paradigm for solving combinatorial optimization problems, but the development of SLS for solving PBO is still in its infancy. In this paper, we develop an effective SLS algorithm for solving PBO, dubbed NuPBO, which introduces a novel scoring function for PB constraints and a new weighting scheme. We conduct experiments on a broad range of six public benchmarks, including three real-world benchmarks, a benchmark from PB competition, an integer linear programming optimization benchmark, and a crafted combinatorial benchmark, to compare NuPBO against five state-of-the-art competitors, including a recently-proposed SLS PBO solver LS-PBO, two complete PB solvers PBO-IHS and RoundingSat, and two mixed integer programming (MIP) solvers Gurobi and SCIP. NuPBO has been exhibited to perform best on these three real-world benchmarks. On the other three benchmarks, NuPBO shows competitive performance compared to state-of-the-art competitors, and it significantly outperforms LS-PBO, indicating that NuPBO greatly advances the state of the art in SLS for solving PBO.

伪布尔约束具有很强的表达能力，许多组合优化问题都可以用伪布尔优化 (PBO) 来建模。随机局部搜索 (Stochastic Local Search，SLS) 被公认为是求解组合优化问题的有力范式，但用于求解 PBO 的 SLS 的发展仍处于起步阶段。在本文中，我们提出了一种有效的求解 PBO 的 SLS 算法，称为 NuPBO¹，它引入了一种新的打分函数和加权方案。我们在广泛的 6 个 Benchmark 上进行了实验，包括 3 个真实的基准、一个来自 PB 竞争的基准、一个整数线性规划优化基准和一个精心设计的组合基准，以比较 NuPBO 与 5 个最先进的求解器

PBO 问题定义与记号

给定一个变量集合 $X=\{x_1,\dots ,x_n\},x_i\in \{0,1\}$，一个 PBO 问题的形式如下

$$\begin{array}{rl}\underset{\{x_1,\dots ,x_n\}}{\min }& \sum _{i=1}^n{c}_i\cdot l_i,c_i\in \mathbb{Z}\\ s.t.& \underset{j=1}{\overset{m}{\bigwedge }}\sum _{i=1}^n{a}_{ji}\cdot l_i\ge b_j,a_{ji},b_j\in {\mathbb{N}}_0^{+}\end{array}$$

Hint

注意，这里我们的约束只考虑了 $\ge$ 的形式，这是因为 $\le ,=$ 的形式能够通过文字的取反来快速转化为 $\ge$ 的形式

这里，对于任意一个给定的赋值 $\alpha$，其目标函数的值我们记为 $obj(\alpha )$，如果一个赋值 ${\alpha }_1$ 比赋值 ${\alpha }_2$ 更好，那么必然有 $obj({\alpha }_1)<obj({\alpha }_2)$

进一步的，我们还引入了一个新概念：PB 约束 $c$ 的平均影响系数，我们将其定义为 $av{g}_{coe}(c)=\frac{{\sum }_{j=1}^n{a}_j}{n}$，对于目标函数，我们也规定其的平均影响系数 $av{g}_{coe}(o)=\frac{{\sum }_{j=1}^n{c}_j}{n}$

由于 PB 约束必须满足，于是我们将其规定为硬约束，给定一个赋值 $\alpha$，如果此赋值未满足硬约束 $c$，我们定义其违背值（惩罚值）为：$viol(c)=\max (0,b-{\sum }_{j=1}^n{a}_j{l}_j)$

Note

可以发现，如果一个赋值 $\alpha$ 是可行解的话，那么必然对任意的硬约束 $c$，都有 $viol(c)=0$

采用约束加权策略的 SLS 算法通常保持每个约束的权重。我们用 $w(c)$ 表示每个硬约束 $c$ 的权重，用 $w(o)$ 表示目标函数 $obj$ 的权重

算法主体思路

由于 SLS 算法的搜索方向是由打分函数引导的，通过使用加权方案可以提高评分函数的有效性，于是，我们首先提出了一个新的打分函数，然后设计了一个新的加权方案与之配合。

打分函数

我们假定，当前的 PBO 实例中有 $n$ 条 PB 约束（硬约束），一个目标函数，此时的赋值为 $\alpha$

A Review of Score Function in LS-PBO

我们再次考虑 LS-PBO 中的打分函数：

• 对于硬约束 $c$，我们考虑其惩罚值为 $penalty(c)=w(c)\times viol(c)$，此时，$hscore(x)$ 定义为翻转 $x$ 所带来的惩罚值的减小量
• 对于目标函数，其惩罚值定义为 $penalty(o)=w(o)\times obj(\alpha )$，此时，$oscore(x)$ 定义为翻转 $x$ 所带来的目标函数惩罚值的减少量

我们将其综合考虑： $score(x)=hscore(x)+oscore(x)$

仔细考虑 $hscore(x)$ 的定义，我们可以发现，由于 $viol(c)=\max (0,b-{\sum }_{j=1}^n{a}_j{l}_j)$，对于一些系数较大的约束，$viol(c)$ 的值也会非常大，这回导致我们更加关注这类约束，这显然是不合理的，考虑如下例子：

Example

$c_1:4\neg x_1+x_2+x_3\ge 4,c_2:3\neg x_1+x_2+2x_3\ge 4,c_3:29x_1+15x_2+16x_3\ge 29$，目标函数为 $x_1+\neg x_2$ ，此问题的最优解为 $(0,1,1)$

此时，我们考虑所有约束的权重都是 $1$ 的情况，那么变量的 $hscore$ 均由 $viol$ 决定，假定此时的赋值为 $(0,0,0)$，那么 $score(x_1)=21,score(x_2)=17score(x_3)=17$，随后，我们选择翻转 $x_1$，得到 $(1,0,0)$

此时 $score(x_1)=-21,score(x_2)=3,score(x_3)=3$，此时不论翻转 $x_2$ 还是 $x_3$，搜索的方向都没有朝着最优解的方向进行（也就是我们更倾向于先满足 $c_3$）

于是，我们针对这种情况（显然这种情况是很常见的），通过加入平滑项，引入了新的打分函数：

• 对于硬约束 $c$，其惩罚值定义为 $penalty(c)=\frac{w(c)\times viol(c)}{smooth(c)}$，此时，$hscore(x)$ 定义为翻转 $x$ 所带来的惩罚值的减小量
• 对于目标函数，其惩罚值定义为：$penalty(o)=\frac{w(o)\times obj(\alpha )}{smooth(o)}$，此时，$oscore(x)$ 定义为翻转 $x$ 所带来的目标函数惩罚值的减少量

最终，我们的打分函数为：$score(x)=hscore(x)+oscore(x)$

平滑项

我们使用约束的平均系数来作为平滑项：

• $smooth(c)=[av{g}_{coe}(c)]$
• $smooth(o)=[av{g}_{coe}(o)]$

我们再次考虑先前的例子，我们有：$smooth(c_1)=2,smooth(c_2)=2,smooth(c_3)=20$

当初始赋值为 $(0,0,0)$ 时， $score(x_1)=-3.05，score(x_2)=2.25,score(x_3)=1.3$，此时，我们会翻转 $x_2$ 得到赋值 $(0,1,0)$

随后，$score(x_1)=-3.3,score(x_2)=-2.25,score(x_3)=0.7$，于是我们翻转了 $x_3$，并得到了最优解 $(0,1,1)$

加权方案

加权方案本质上会指导搜索的方向，即更倾向于于可行解还是最优解，当对软约束赋予过大的权重可能使其难以满足所有的硬约束，此时就会导致我们甚至无法找到可行解，算法的求解能力会受到极大的限制。

于是，在 LS-PBO 中，为软约束（也就是目标函数）设置了 上界，用于控制何时更新目标函数的权重，我们的加权方案如下所示：

• 在搜索开始的最开始，每个硬约束的权重被初始化为 $w(c)=1$，目标函数的权重被初始化为 $w(o)=0$
• 随着搜索的进行，当进入到局部最优时，对每个不满足的硬约束 $c$，我们更新为 $w(c)=w(c)+1$，而如果不存在不满足的硬约束（也就是现在是一个可行解），我们更新 $w(o)=w(o)+1$

在开始时，目标函数的权重被初始化为 0，这样算法将首先专注于寻找可行解。如果搜索陷入局部最优，则只在当前赋值 $\alpha$ 为可行解解时增加目标函数的权重

相应地，如果算法能够频繁的找到可行解，那么说明目标函数有更大的概率得到更好的解

算法框架

算法的框架如下图所示：

在最开始，我们初始化 $\alpha =\vec{0}$，并将硬约束的权重都初始化为 $1$，目标函数权重初始化为 $0$

在这里，我们为局部搜索引入了一个参数 $L$，用于控制局部搜索的深度，当连续 $L$ 次都没有找到更好的解时，我们就会考虑重启，否则，我们让其继续搜索

实验结果

Benchmark 选择为：

• PB16²
• MIPLIB³
• CRAFT⁴
• MWCB⁵
• SAP⁵
• WSNO⁵

对比的算法为：

• LS-PBO
• PBO-IHS⁶
• RoundingSAT⁷
• Gurobi⁸
• SCIP⁹

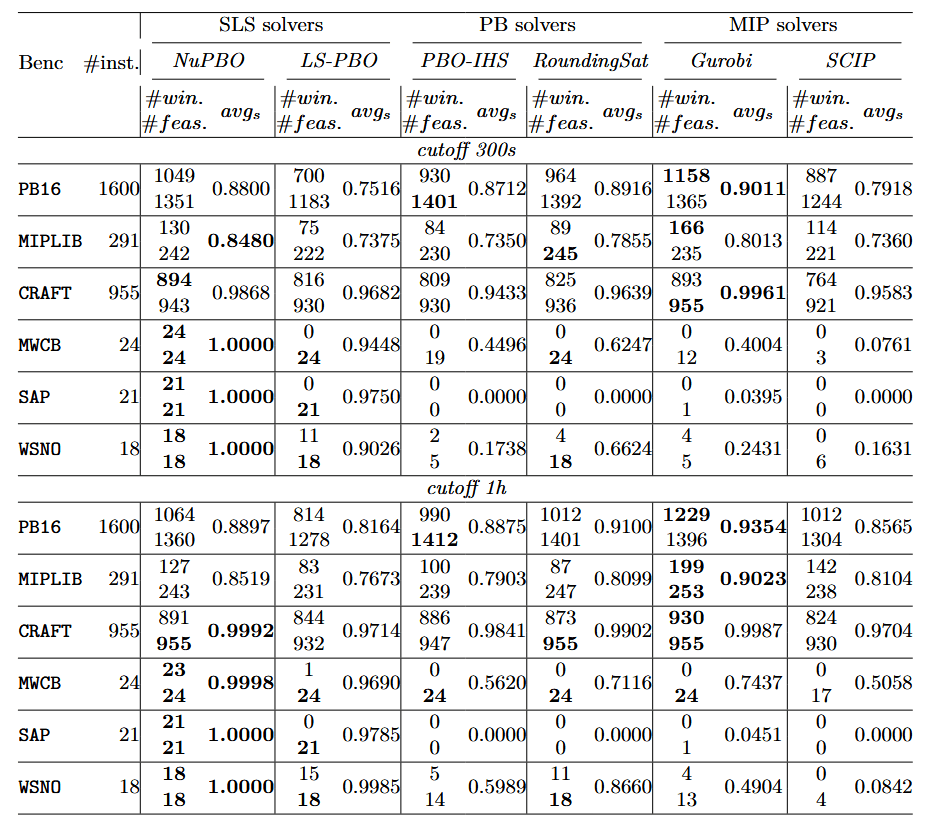
#win 表示通过求解器 $S$ 在实例集合 $B_i$ 上可以得到对应的最优解的实例数(即,获胜实例的数量)

#feas 表示求解器 $S$ 在实例集合 $B_i$ 上获得解的实例数

实验结果如下所示：

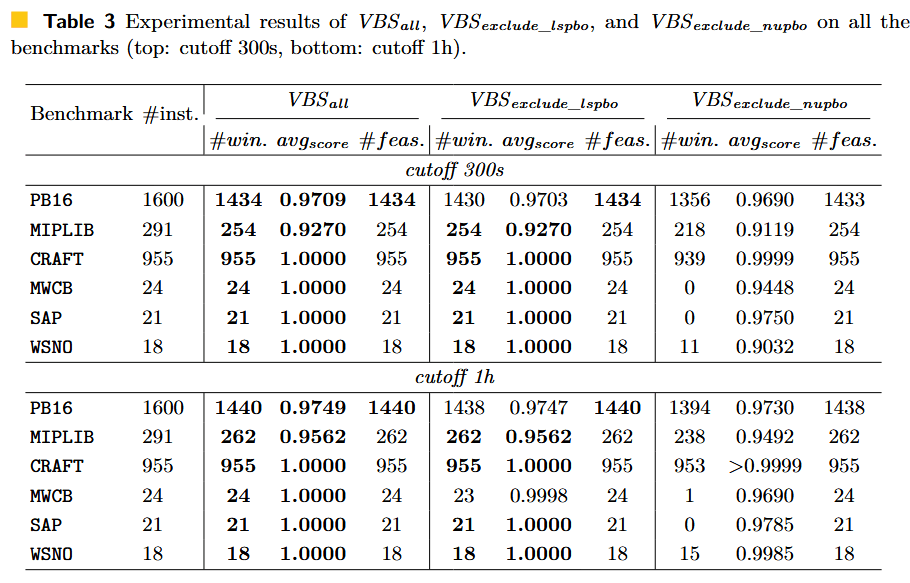
下面这张图通过以下规则进行考虑：

给定一个求解器集合 $\Theta$，对于每一个实例，在 $\Theta$ 上中选择表现最好的求解器进行求解，我们构造的求解器集合为：

$VB{S}_{all}=\{LS\_PBO,NuPBO,PBO\_IHS,RoundingSat,Gurobi,SCIP\}$，$VB{S}_{exclude\_lspbo}=\{NuPBO,PBO\_IHS,RoundingSat,Gurobi,SCIP\}$，$VB{S}_{exclude\_nupbo}=\{LS\_PBO,PBO\_IHS,RoundingSat,Gurobi,SCIP\}$

可以发现，缺少了 NuPBO 后，求解能力下降了很多

Remarque

1. 源代码可见 NuPBO ↩

2. http://www.cril.univ-artois.fr/PB16/bench/PB16-used.tar ↩

3. https://zenodo.org/record/3870965 ↩

4. https://zenodo.org/record/4036016 ↩

5. https://lcs.ios.ac.cn/%7ecaisw/Resource/LS-PBO/ ↩ ↩² ↩³

6. https://bitbucket.org/coreo-group/pbo-ihs-solver/ ↩

7. https://doi.org/10.5281/zenodo.4043124 ↩

8. https://www.gurobi.com/products/gurobi-opti ↩

9. https://www.scipopt.org/index.php#download ↩