基础加密算法

Description

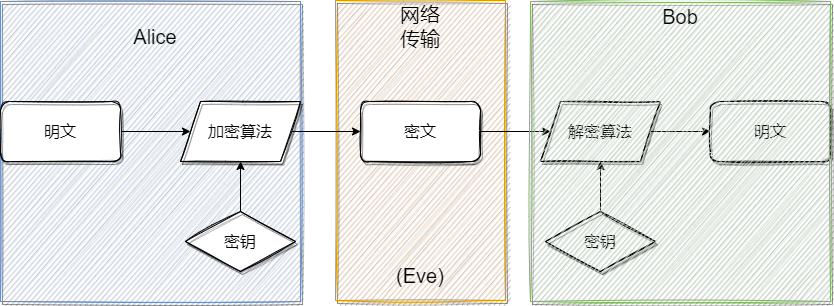
Alice 和 Bob 很久没见面了，他们十分想念彼此。因此有一天，Alice 写了一封信 Message 送给 Bob，但有一个坏家伙 Eve 想偷窥这封信，看看到底写了什么。但 Alice 希望即使 Eve 得到了这封信他也看不明白写了什么，这样他就只能乖乖交给 Bob。所以 Alice 希望你给出一个算法，使得只有 Alice 和 Bob 能通过算法看懂 Message。

显然，这个算法就是 加密算法，Alice 通过加密算法将明文加密为密文，而 Bob 通过算法将其还原。对于Eve而言，他永远不知道 Alice 究竟写了什么。

题外话，对密码学感兴趣的朋友可以看看这本入门教材 An Introduction to Mathematical Cryptography，书的 pdf 版本可以在 zlibary(需要科学上网)

现代的加密算法包括三种类型：

1. 对称加密，例如 DES, 3DES, AES
2. 非对称加密，例如著名的 RSA
3. 还有一种散列算法，事实上这种算法并不能算做是加密，它更像是一种摘要。

密码散列

这里主要介绍 MD5 算法。

MD5算法具有以下特点：

1. 压缩性：任意长度的数据，算出的 MD5 值长度都是固定的。
2. 容易计算：从原数据计算出 MD5 值很容易。
3. 抗修改性：对原数据进行任何改动，哪怕只修改 1 个字节，所得到的 MD5 值都有很大区别。
4. 强抗碰撞：已知原数据和其 MD5 值，想找到一个具有相同 MD5 值的数据（即伪造数据）是非常困难的。

类似 MD5 的这些密码散列算法几乎都是单向算法，也就是说根据输出结果不可能反推出输入信息。网上类似 MD5 解密的大多都是暴力破解，在庞大的数据库中暴力比对碰撞，碰撞成功了就认为解密成功了。也可以构造出两份 MD5 完全相同的明文，例如，我们我们可以构造出两个文件 A、B，使得 md5(A) = md5(B)。但是如果指定一份文件 A，构造一份文件 B，使得 md5(A) = md5(B)，这在目前来说还是不行。

MD5 加密过程

填充

在 MD5 算法中，首先需要对信息进行填充，使其位长对 512 求余的结果等于 448，并且填充必须进行，即使其位长对 512 求余的结果等于 448。因此，信息的位长（Bits Length）将被扩展至 $N\ast 512+448$，$N$ 为一个非负整数。

填充的方法如下：

1. 在信息的后面补一个 1，然后补 0 至满足上述要求，总共最少要补 1bit，最多补 512bit。
2. 在这个结果后面附加一个以 64 位二进制表示的填充前信息长度，如果二进制表示的填充前信息长度超过 64 位，则取低 64 位。

经过这两步的处理，信息的位长为 $N\ast 512+448+64=(N+1)\ast 512$，即长度恰好是 512 的整数倍。于是，我们能将消息分为共 $N+1$ 组。

初始化缓冲器

用一个四个字的缓冲器(A，B，C，D)来计算报文摘要，A,B,C,D 分别是 32 位的寄存器，初始化使用的是十六进制表示的数字，注意低字节在前（大端法）： word A: 01 23 45 67 word B: 89 ab cd ef word C: fe dc ba 98 word D: 76 54 32 10

注意，在程序中，应写为：0x67452301, 0xefcdab89, 0x98badcfe, 0x10325476

转换

将每一分组被划分为 16 个 32 位子分组，对每一分组进行四轮运算转化。

首先定义 4 个辅助函数，这四个函数输入是一个 32 位的字，输出也是一个 32 位的字。

1
  F(X,Y,Z) = (X & Y) | (( ~ X) & Z)
2
  G(X,Y,Z) = (X & Z) | (Y & ( ~ Z))
3
  H(X,Y,Z) = X ^ Y ^ Z
4
  I(X,Y,Z) = Y ^ (X | ( ~ Z))

假设$M_j$表示消息的第 $j$ 个子分组（从 0 到 15），常数 $t_i$ 是 $4294967296\ast abs(\sin (i))$ 的整数部分，i 取值从 1 到 64，单位是弧度。

我们定义四种操作：

$$FF(a,b,c,d,Mj,s,ti)\to a=b+((a+F(b,c,d)+M_j+t_i)<<<s)$$ $$GG(a,b,c,d,Mj,s,ti)\to a=b+((a+G(b,c,d)+M_j+t_i)<<<s)$$ $$HH(a,b,c,d,Mj,s,ti)\to a=b+((a+H(b,c,d)+M_j+t_i)<<<s)$$ $$II(a,b,c,d,Mj,s,ti)\to a=b+((a+I(b,c,d)+M_j+t_i)<<<s)$$

那么，这四轮是：

第一轮

$$FF(a,b,c,d,M0,7,0xd76aa478)$$ $$FF(d,a,b,c,M1,12,0xe8c7b756)$$ $$FF(c,d,a,b,M2,17,0x242070db)$$ $$FF(b,c,d,a,M3,22,0xc1bdceee)$$ $$FF(a,b,c,d,M4,7,0xf57c0faf)$$ $$FF(d,a,b,c,M5,12,0x4787c62a)$$ $$FF(c,d,a,b,M6,17,0xa8304613)$$ $$FF(b,c,d,a,M7,22,0xfd469501)$$ $$FF(a,b,c,d,M8,7,0x698098d8)$$ $$FF(d,a,b,c,M9,12,0x8b44f7af)$$ $$FF(c,d,a,b,M10,17,0xffff5bb1)$$ $$FF(b,c,d,a,M11,22,0x895cd7be)$$ $$FF(a,b,c,d,M12,7,0x6b901122)$$ $$FF(d,a,b,c,M13,12,0xfd987193)$$ $$FF(c,d,a,b,M14,17,0xa679438e)$$ $$FF(b,c,d,a,M15,22,0x49b40821)$$

第二轮

$$GG(a,b,c,d,M1,5,0xf61e2562)$$ $$GG(d,a,b,c,M6,9,0xc040b340)$$ $$GG(c,d,a,b,M11,14,0x265e5a51)$$ $$GG(b,c,d,a,M0,20,0xe9b6c7aa)$$ $$GG(a,b,c,d,M5,5,0xd62f105d)$$ $$GG(d,a,b,c,M10,9,0x02441453)$$ $$GG(c,d,a,b,M15,14,0xd8a1e681)$$ $$GG(b,c,d,a,M4,20,0xe7d3fbc8)$$ $$GG(a,b,c,d,M9,5,0x21e1cde6)$$ $$GG(d,a,b,c,M14,9,0xc33707d6)$$ $$GG(c,d,a,b,M3,14,0xf4d50d87)$$ $$GG(b,c,d,a,M8,20,0x455a14ed)$$ $$GG(a,b,c,d,M13,5,0xa9e3e905)$$ $$GG(d,a,b,c,M2,9,0xfcefa3f8)$$ $$GG(c,d,a,b,M7,14,0x676f02d9)$$ $$GG(b,c,d,a,M12,20,0x8d2a4c8a)$$

第三轮

$$HH(a,b,c,d,M5,4,0xfffa3942)$$ $$HH(d,a,b,c,M8,11,0x8771f681)$$ $$HH(c,d,a,b,M11,16,0x6d9d6122)$$ $$HH(b,c,d,a,M14,23,0xfde5380c)$$ $$HH(a,b,c,d,M1,4,0xa4beea44)$$ $$HH(d,a,b,c,M4,11,0x4bdecfa9)$$ $$HH(c,d,a,b,M7,16,0xf6bb4b60)$$ $$HH(b,c,d,a,M10,23,0xbebfbc70)$$ $$HH(a,b,c,d,M13,4,0x289b7ec6)$$ $$HH(d,a,b,c,M0,11,0xeaa127fa)$$ $$HH(c,d,a,b,M3,16,0xd4ef3085)$$ $$HH(b,c,d,a,M6,23,0x04881d05)$$ $$HH(a,b,c,d,M9,4,0xd9d4d039)$$ $$HH(d,a,b,c,M12,11,0xe6db99e5)$$ $$HH(c,d,a,b,M15,16,0x1fa27cf8)$$ $$HH(b,c,d,a,M2,23,0xc4ac5665)$$

第四轮

$$II(a,b,c,d,M0,6,0xf4292244)$$ $$II(d,a,b,c,M7,10,0x432aff97)$$ $$II(c,d,a,b,M14,15,0xab9423a7)$$ $$II(b,c,d,a,M5,21,0xfc93a039)$$ $$II(a,b,c,d,M12,6,0x655b59c3)$$ $$II(d,a,b,c,M3,10,0x8f0ccc92)$$ $$II(c,d,a,b,M10,15,0xffeff47d)$$ $$II(b,c,d,a,M1,21,0x85845dd1)$$ $$II(a,b,c,d,M8,6,0x6fa87e4f)$$ $$II(d,a,b,c,M15,10,0xfe2ce6e0)$$ $$II(c,d,a,b,M6,15,0xa3014314)$$ $$II(b,c,d,a,M13,21,0x4e0811a1)$$ $$II(a,b,c,d,M4,6,0xf7537e82)$$ $$II(d,a,b,c,M11,10,0xbd3af235)$$ $$II(c,d,a,b,M2,15,0x2ad7d2bb)$$ $$II(b,c,d,a,M9,21,0xeb86d391)$$

所有这些完成之后，a、b、c、d 分别在原来基础上再加上 A、B、C、D，然后用下一分组数据继续运行以上算法。

经过程序流程，生成四个 32 位数据（也就是最终的 a, b, c, d），最后联合起来成为一个 128-bits 散列数据，这样 MD5的工作就做完了。

代码可详见 topdeoo/encryption-algorithm (github.com)

对称加密

什么叫对称加密？这里需要先引入 密钥 的概念。

密钥是一种参数，它是在明文转换为密文或将密文转换为明文的算法中输入的参数 ——来自百度

也就是说，加密函数通过密钥加密，解密函数通过密钥解密。

那么在对称加密中， Alice 和 Bob 共享一个密钥，也就是说，Alice 通过密钥将明文加密，Bob 通过相同的密钥将密文解开，知道 Alice 想说什么。

当双方的密钥完全相同时，就称之为 对称加密。

当前最常使用的对称加密算法是 AES 算法，微信中的加密传输使用的就是这种。

但对称加密的不足也很明显：Alice 和 Bob 需要同时知道密钥是什么，而密钥要么提前约定好，要么随着密文一起传送。所以在现代加密中，我们通常通过非对称加密算法传输对称加密的密钥，随后，通过对称加密算法来传输信息。

RSA

RSA 是经典的非对称加密算法，也是当前最能耳熟能详的加密算法，RSA 是 1977 年由罗纳德·李维斯特（Ron Rivest）、阿迪·萨莫尔（Adi Shamir）和伦纳德·阿德曼（Leonard Adleman）一起提出的。

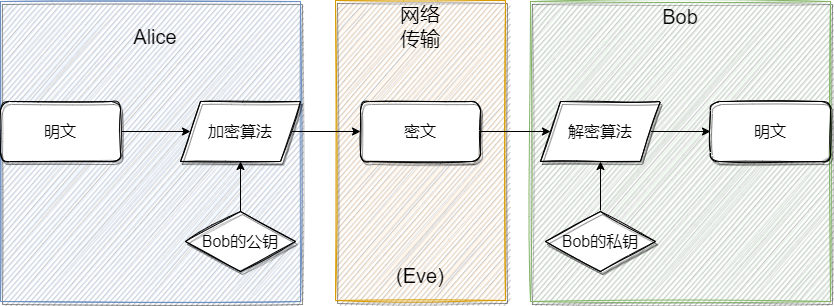
通过一张流程图来描述 RSA 算法到底做了什么：

可以发现，重点在于 公钥 与 私钥 的变化上，这也是为什么 RSA 被称为非对称加密的原因。

注意，公钥是可以被任何人知道的，而私钥必须被保密，因此我们不需要像对称加密的那样担心密钥的传输。

为了打造这两把钥匙，一把用于上锁，一把用于开锁，我们需要一些数学的前置知识。

数学基础

一些前置知识：

• 素数

• 同余

  同余，意味余同，也就是余数相同的意思，我们通常使用 $a\equiv b(modp)$ 来表示，意味 $a$ 除以 $p$ 的余数与 $b$ 除以 $p$ 的余数相等，或也可以视为$p$ 整除 $a-b$，例如 $1\equiv 4(mod3)$。

  同余式可以互相加：若$a\equiv b(modp)$， $c\equiv d(modp)$，则 $a+c\equiv b+d(modp)$

  同余式可以互相乘：若$a\equiv b(modp)$，$c\equiv d(modp)$，则 $ac\equiv bd(modp)$

欧拉函数

欧拉函数的出现来源于一个问题：

给定任意正整数 $n$，问从 1 到 $n$ 中，与 $n$ 互质的数共有多少个？(注意互质的定义是除了 1 以外没有其他公因子，因此 $1$ 与其他正整数都互质)

答案可以用 $\phi (n)$ 来表示。

这个问题其实很好解决，既然条件是互质，那么显然我们可以对 $n$ 进行分类：

1. $n$ 为素数

   若 $n$ 为素数，显然 $n$ 与不为 $n$ 的数都互质，于是 $\phi (n)=n-1$

2. $n$ 不为素数

   我们可以发现一个事实：

   任何一个正整数 $n(n\ge 2)$ 都可以写成如下的形式：$n=p_1^{{\alpha }_1}{p}_2^{{\alpha }_2}\dots p_t^{{\alpha }_t}$，其中 $p_i(i=1,2,\dots ,t)$ 为素数， ${\alpha }_i(i=1,2,\dots ,t)\ge 0$

   也就是说，任何一个正整数都可以唯一写成有限个素数乘积的形式。例如，$24$ 可以写为 $24=2^3\ast 3$

   这个事实被称为 素数唯一分解定理（这里略去证明过程）

   那么基于这个定理，于是我们可以将 $n$ 分解为 $p_1^{{\alpha }_1}{p}_2^{{\alpha }_2}\dots p_t^{{\alpha }_t}$ 的形式，于是 $\phi (n)=\phi (p_1^{{\alpha }_1}{p}_2^{{\alpha }_2}\dots p_t^{{\alpha }_t})=\phi (p_1^{{\alpha }_1})\phi (p_2^{{\alpha }_2})\dots \phi (p_t^{{\alpha }_t})$ 。（第二个等号的成立基于 中国剩余定理）

   于是，我们只需要知道 $\phi (p^k)$ 如何求即可。

   由于与 $p^k$ 互质的数太多且没什么规律，因此我们可以换个角度来计算 $\phi (p^k)$ ：我们先计算与 $p^k$ 不互质的即可。

   而这些数所共有的特征是显然的：这些数都存在质因子 $p^i(i=1,2,\dots ,k)$ ，我们列出来，也就是 $1\times p,2\times p,3\times p\dots ,p^{(k-1)}\times p$，共有 $p^{(k-1)}$ 个，我们将这些数去除，剩余的便都是与 $p^k$ 互质的数了。

   于是 $\phi (p^k)=p^k-p^{(k-1)}=p^k(1-\frac{1}{p})$

   于是$\phi (n)=\phi (p_1^{{\alpha }_1}{p}_2^{{\alpha }_2}\dots p_t^{{\alpha }_t})=\phi (p_1^{{\alpha }_1})\phi (p_2^{{\alpha }_2})\dots \phi (p_t^{{\alpha }_t})=p_1^{{\alpha }_1}(1-\frac{1}{p_1})p_2^{{\alpha }_2}(1-\frac{1}{p_2})\dots p_t^{{\alpha }_t}(1-\frac{1}{p_t})=n(1-\frac{1}{p_1})(1-\frac{1}{p_2})\dots (1-\frac{1}{p_t})$

这样，我们就推导出了欧拉函数的解析式：

$$\phi (n)=\{\begin{array}{l}n-1ifnisprime,\\ n(1-\frac{1}{p_1})(1-\frac{1}{p_2})\dots (1-\frac{1}{p_t})otherwise\end{array}$$

以 $\phi (24)$ 为例，我们计算为 $\phi (24)=24\ast (1-\frac{1}{2})\ast (1-\frac{1}{3})=8$

欧拉定理

若 $(a,n)=1$（即两数互质），则 $a^{\phi (n)}\equiv 1(modn)$。

可以发现当 $n$ 为素数时，这就是费马小定理。

逆元

如果两个正整数 $a$ 和 $n$ 互质，那么一定可以找到整数 $b$，使得 $ab-1$ 被 $n$ 整除， 即 $ab\equiv 1(modn)$

此时，称 $b$ 为 $a$ 关于 $n$ 的乘法逆元，记为 $a^{-1}$

RSA 算法

密钥的构建

现在，我们可以开始构建 Bob 的两把钥匙了。

第一把是公钥，用于加密，送给 Alice；第二把是私钥，用于解密，Bob 会自己留着。

1. Bob 随机生成了两个非常大的质数 $p$ 与 $q$ ，其中 $p\ne q$。

2. Bob 计算了这两个质数的乘积 $n=pq$

   注意，这个 $n$ 的二进制长度就是密钥的长度。实际应用中，RSA 的密钥长度通常选择 1024，甚至 2048。

3. Bob 计算了欧拉函数 $\phi (n)=(p-1)(q-1)$

   由于 n 太大了，并且我们无法在多项式时间内完成质因数分解（这是一个典型的 NP 问题）

   因此，任何人都无法利用 n 推出$\phi (n)$。

   $\phi (n)$ 的值只有 Bob 自己知道。

   这就是 RSA 难以破解的理论保证。

4. Bob 随机选择了一个数 $e$ ，满足 $1<e<\phi (n)$ 且 $e\ne p,q$，且 $(e,\phi (n))=1$

   实际应用中常选择 $e=65537$

5. Bob 计算了 $e$ 关于 $\phi (n)$ 的乘法逆元 $d$， 即 $ed\equiv 1(mod\phi (n))$， 也就是说 $ed=k\phi (n)+1$

至此，Bob 完成了所有的计算，我们的两把钥匙也构造好了：

对于任意一个与 $n$ 互质的数 $a$ ，由于欧拉定理，我们有：

$$a^{\phi (n)}\equiv 1(modn)$$ $$\to a^{k\phi (n)}\equiv 1(modn)$$ $$\to a^{k\phi (n)+1}\equiv a(modn)$$ $$\to a^{ed}\equiv a(modn)$$

所以，若 $c\equiv a^e(modn)$， 则 $c^d\equiv a^{ed}\equiv a(modn)$

这样，我们得到公钥为 $(n,e)$， 私钥为 $(n,d)$

接下来，我们就可以对一份明文进行加密与解密了。

加密与解密

对于一份明文 $a$ ，Alice 利用公钥 $(n,e)$ 加密，使其变为密文 $c$ ，具体而言，Alice 将：

• 计算出 $c\equiv a^e(modn)$ 中的 $c$ 即可

  这是很简单的，我们只需要计算 $a^e$ 并对 $n$ 取模即可

随后，Bob 只需要用私钥对 $c$ 进行解密，具体而言，Bob 将：

• 计算出 $a\equiv c^d(modn)$ 中的 $a$ 即可

从头到尾，除了 Bob，没有任何人可以知道$\phi (n)$，所以没有人可以求出 $e$ 关于 $\phi (n)$ 的乘法逆元 $d$ 。也就是说 $d$ 的值从头到尾只有 Bob 自己知道，不可能泄露。

注意，上述的 $a$ 不能超过 $n$。

举个例子，我们如何对 $abcd$ 进行加密呢？

1. 首先，我们需要对 $abcd$ 进行映射的排列，具体为 $a$ 映射到 $00$ ，$b$ 映射到 $01$ ……。于是，我们得到 $00010203$
2. 随后，我们对映射完的字符串进行分块，每一块转为十进制整数的大小不能超过 $n$ ，一般而言，若RSA密钥长度为 M bit，分段加密字节数为$\frac{M}{8}-11$，分段解密字节数为 $\frac{M}{8}$
3. 接下来，我们对每一块进行 RSA 加密，即计算这个整数的 $e$ 次幂模 $n$ ，得到密文
4. 最后将密文拼接起来即可

在实际应用中，我们需要加密的信息不可能那么短，所以一般的选择都是通过 RSA 来传送 AES 的密钥，而真正的信息是通过 AES 来传输。

RSA 的代码详见 topdeoo/encryption-algorithm (github.com)